
【题目】阳阳超市以每件10元的价格购进了一批玩具,定价为20元时,平均每天可售出80个.经调查发现,玩具的单价每降1元,每天可多售出40个;玩具的单价每涨1元,每天要少售出5个.如何定价才能使每天的利润最大?求出此时的最大利润.
【答案】当定价为16元时,每天的利润最大,最大利润是1440元
【解析】
分降价和涨价两种情形,根据利润公式“![]() ”列出等式,再根据二次函数的性质求解即可.
”列出等式,再根据二次函数的性质求解即可.
由题意,需分降价和涨价两种情形:
(1)在降价的情况下,设每件降价![]() 元,则每天的利润为
元,则每天的利润为![]() 元
元
则![]()
整理得:![]()
由二次函数图象的性质可得:当![]() 时,
时,![]() 取得最大值1440
取得最大值1440
故当定价为16元时,才能使每天的利润最大,最大利润为1440元
(2)在涨价的情况下,设每件涨价![]() 元,则每天的利润为
元,则每天的利润为![]() 元
元
则![]()
整理得:![]()
由二次函数图象的性质可得:当![]() 时,
时,![]() 取得最大值845
取得最大值845
故当定价为23元时,才能使每天的利润最大,最大利润为845元
综上,当定价为16元时,才能使每天的利润最大,最大利润为1440元


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点B、C,经过B、C两点的抛物线
轴分别相交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A,顶点为P,且对称轴为直线
轴的另一个交点为A,顶点为P,且对称轴为直线![]() 。点G是抛物线
。点G是抛物线![]() 位于直线
位于直线![]() 下方的任意一点,连接PB、GB、GC、AC .
下方的任意一点,连接PB、GB、GC、AC .
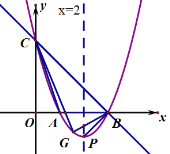
(1)求该抛物线的解析式;
(2)求△GBC面积的最大值;
(3)连接AC,在![]() 轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华书店销售一个系列的儿童书刊,每套进价100元,定价为140元,一天可以销售20套.为了扩大销售,增加盈利,减少库存,书店决定采取降价措施.若一套书每降价0.5元,平均每天可多售出1套.设每套书降价x元时,书店一天可获利润y元.
(1)求出y与x的函数关系式;
(2)该书店要获得最大利润,售价应定为每套多少元?
(3)小静说:“当某天的利润最大时,当天的销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
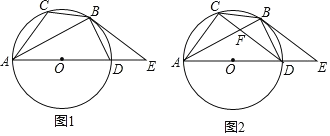
(1)如图1,若BD=![]() ,AC=6
,AC=6
A.求证:BE为圆O的切线
B.求DE的长
(2)如图2,连结CD交AB于点F,若BD=![]() ,CF=3,求圆O的半径.
,CF=3,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(![]() ,
, ![]() )、Q(
)、Q(![]() ,
, ![]() )是该反比例函数图象上的两点,且
)是该反比例函数图象上的两点,且![]() 时,
时, ![]() ,指出点P、Q各位于哪个象限?并简要说明理由.
,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,消费者在网店购买某种商品后,对其有
“好评”、“中评”、“差评”三种评价,假设这三种评价是等可能的.

(1)小明对一家网店销售某种商品显示的评价信息进行了统计,并列出了两幅不完整的统计图.
利用图中所提供的信息解决以下问题:
①小明一共统计了 个评价;
②请将图1补充完整;
③图2中“差评”所占的百分比是 ;
(2)若甲、乙两名消费者在该网店购买了同一商品,请你用列表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①b2﹣4ac<0;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③3a+c=0;
④当y>0时,x的取值范围是﹣1<x<3;⑤当x>0时,y随x增大而减小.
其中结论正确的个数是( )
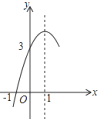
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(k﹣1)x2+(2k+1)x+k=0.
(1)依据k的取值讨论方程解的情况.
(2)若方程有一根为x=﹣2,求k的值及方程的另一根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )
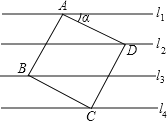
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com