
 2017年初,合肥市积极推进共享单车服务(如图1),努力创造绿色环保出行,图2是某品牌单车的车架示意图,其中ED=40cm,∠DEF=60°,∠F=45°,求传动轮轴心E到后轮轴心F的距离EF的长.(结果精确到1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
2017年初,合肥市积极推进共享单车服务(如图1),努力创造绿色环保出行,图2是某品牌单车的车架示意图,其中ED=40cm,∠DEF=60°,∠F=45°,求传动轮轴心E到后轮轴心F的距离EF的长.(结果精确到1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 分析 如图2中,作DH⊥EF于H.在Rt△EDH中,根据sin∠DEH=$\frac{DH}{DE}$,cos∠DEH=$\frac{EH}{DE}$,求出DH、EH,在Rt△DHF中,由∠F=45°,可得HF=DH=20$\sqrt{3}$cm,根据EF=EH+HF计算即可.
解答 解:如图2中,作DH⊥EF于H.
在Rt△EDH中,∵sin∠DEH=$\frac{DH}{DE}$,
∴DH=DE×sin40°=40×$\frac{\sqrt{3}}{2}$=20$\sqrt{3}$cm,
∵cos∠DEH=$\frac{EH}{DE}$,
∴EH=DE×cos60°=40×$\frac{1}{2}$=20cm,
在Rt△DHF中,∵∠F=45°,
∴HF=DH=20$\sqrt{3}$cm,
∴EF=EH+HF=20+20$\sqrt{3}$≈55cm,
∴传动轮轴心E到后轮轴心F的距离EF的长约为55cm.
点评 本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线面构造直角三角形解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
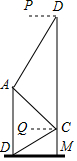 如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
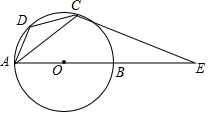 如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.
如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
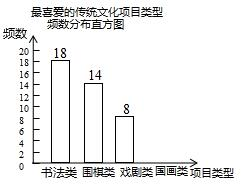 某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.| 项目类型 | 频数 | 频率 |
| 书法类 | 18 | a |
| 围棋类 | 14 | 0.28 |
| 喜剧类 | 8 | 0.16 |
| 国画类 | b | 0.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
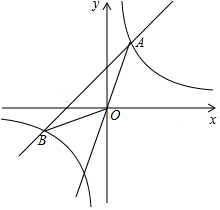 如图,直线y=4x与反比例函数y=$\frac{k}{x}$(k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=$\frac{1}{4}$.
如图,直线y=4x与反比例函数y=$\frac{k}{x}$(k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=$\frac{1}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com