【题目】已知
是
的直径，
，
、
分别与圆相交于
、
，那么下列等式中一定成立的是（ ）
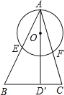
A. AEBF=AFCF B. AEAB=AOAD'
C. AEAB=AFAC D. AEAF=AOAD
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案科目：初中数学 来源： 题型：
【题目】某校为了解本校学生每周参加课外辅导班的情况，随机调査了部分学生一周内参加课外辅导班的学科数，并将调查结果绘制成如图1、图2所示的两幅不完整统计图（其中A：0个学科，B：1个学科，C：2个学科，D：3个学科，E：4个学科或以上），请根据统计图中的信息，解答下列问题：
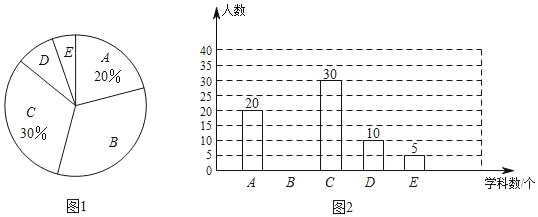
（1）请将图2的统计图补充完整；
（2）根据本次调查的数据，每周参加课外辅导班的学科数的众数是 个学科；
（3）若该校共有2000名学生，根据以上调查结果估计该校全体学生一周内参加课外辅导班在3个学科（含3个学科）以上的学生共有 人．
查看答案和解析>>
科目：初中数学 来源： 题型：
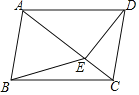
【题目】如图，在四边形ABCD中，AB∥CD，∠ABC＝∠ADC，DE垂直于对角线AC，垂足是E，连接BE．
（1）求证：四边形ABCD是平行四边形；
（2）若△ABE是等边三角形，四边形BCDE的面积等于2
，求CE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
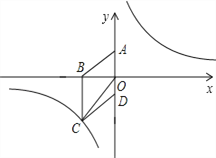
【题目】如图，在平面直角坐标系中，已知四边形ABCD为菱形，且
（0，3）、
（﹣4，0）．
（1）求经过点
的反比例函数的解析式；
（2）设
是（1）中所求函数图象上一点，以
顶点的三角形的面积与△COD的面积相等．求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果一个三角形的两条边的和是第三边的两倍，则称这个三角形是“优三角形”，这两条边的比称为“优比”（若这两边不等，则优比为较大边与较小边的比），记为
.
（1）命题：“等边三角形为优三角形，其优比为1”，是真命题还是假命题？
（2）已知
为优三角形，
，
，
，
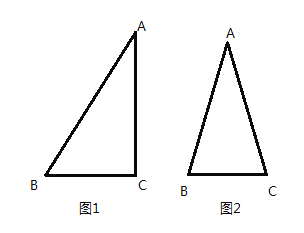
①如图1，若
，
，
，求
的值.
②如图2，若
，求优比的取值范围.
（3）已知是优三角形，且
，
，求的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于一元二次方程
，下列说法：①若
，则方程必有一根为
；②若
是方程的一个根，则一定有
成立；③若
，则方程一定有两个不相等实数根；其中正确结论有（ ）个．
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
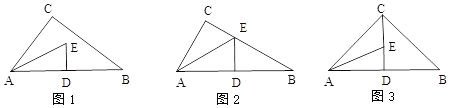
【题目】如图1，△ABC是直角三角形，∠C=90°，∠CAB的角平分线AE与 AB的垂直平分线DE相交于点E.
（1）如图2，若点E正好落在边BC上.
①求∠B的度数
②证明：BC=3DE
（2）如图3，若点E满足C、E、D共线.
求证：AD+DE=BC.
查看答案和解析>>
科目：初中数学 来源： 题型：
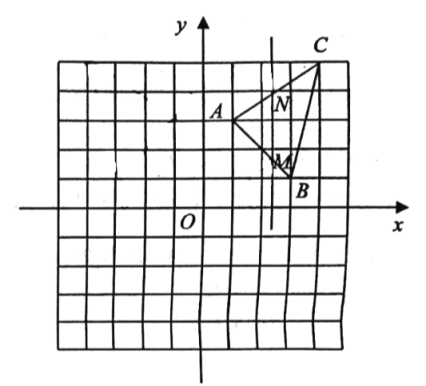
【题目】如图，在平面直角坐标系中，点
，点
，点
.
（1）画出
关于
轴的对称图形
，并写出点
的对称点
的坐标；
（2）若点
在
轴上，连接
、
，则
的最小值是 ；
（3）若直线
轴，与线段
、
分别交于点
、
（点不与点重合），若将
沿直线
翻折，点的对称点为点
，当点落在的内部（包含边界）时，点的横坐标
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
