
【题目】如图,直线y=![]() x+
x+![]() 与两坐标轴分别交于A、B两点.
与两坐标轴分别交于A、B两点.
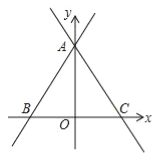
(1)求∠ABO的度数;
(2)过A的直线l交x轴半轴于C,AB=AC,求直线l的函数解析式.
【答案】(1)∠ABO=60°;(2)y=﹣![]() x+
x+![]() .
.
【解析】
试题分析:(1)根据一次函数解析式y=![]() x+
x+![]() 求出点A、B的坐标,在Rt△ABO中,求出tan∠ABO的值,从而求出∠ABO的度数;(2)根据题意可得,AB=AC,AO⊥BC,可得AO为BC的中垂线,根据点B的坐标,求得点C的坐标,利用待定系数法求出直线l的函数解析式即可.
求出点A、B的坐标,在Rt△ABO中,求出tan∠ABO的值,从而求出∠ABO的度数;(2)根据题意可得,AB=AC,AO⊥BC,可得AO为BC的中垂线,根据点B的坐标,求得点C的坐标,利用待定系数法求出直线l的函数解析式即可.
试题解析:(1)对于直线y=![]() x+
x+![]() ,
,
令x=0,则y=![]() ,
,
令y=0,则x=﹣1,
故点A的坐标为(0,![]() ),点B的坐标为(﹣1,0),
),点B的坐标为(﹣1,0),
则AO=![]() ,BO=1,
,BO=1,
在Rt△ABO中,
∵tan∠ABO=![]() =
=![]() ,
,
∴∠ABO=60°;
(2)在△ABC中,
∵AB=AC,AO⊥BC,
∴AO为BC的中垂线,
即BO=CO,
则C点的坐标为(1,0),
设直线l的解析式为:y=kx+b(k,b为常数),
则![]() ,
,
解得:![]() ,
,
即函数解析式为:y=﹣![]() x+
x+![]() .
.


科目:初中数学 来源: 题型:
【题目】为了考察某七年级男生的身高情况,调查了60名男生的身高,那么它的总体是________,个体是______________,总体的一个样本是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查适合作普查的是 ( ).
A. 了解在校大学生的主要娱乐方式
B. 了解某市居民对废电池的处理情况
C. 日光灯管厂要检测一批灯管的使用寿命
D. 对甲型H7N9流感患者的同一车厢的乘客进行医学检查
查看答案和解析>>
科目:初中数学 来源: 题型:
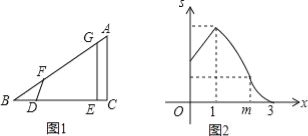
【题目】如图1,△ABC中,∠C=90°,线段DE在射线BC上,且DE=AC,线段DE沿射线BC运动,开始时,点D与点B重合,点D到达点C时运动停止,过点D作DF=DB,与射线BA相交于点F,过点E作BC的垂线,与射线BA相交于点G.设BD=x,四边形DEGF与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤m,1<x≤m,m<x≤3时,函数的解析式不同)
(1)填空:BC的长是 ;
(2)求S关于x的函数关系式,并写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com