
 如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )
如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )| 3 |
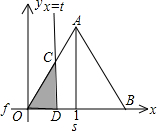
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
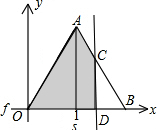
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |


科目:初中数学 来源:2013年初中数学单元提优测试卷-相似的性质(带解析) 题型:单选题
如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )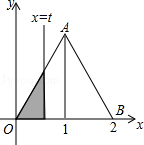
A. | B. | C. | D.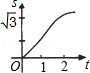 |
查看答案和解析>>
科目:初中数学 来源:2008年江苏省淮安市淮阴中学高一分班考试数学试卷(解析版) 题型:选择题




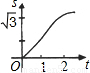
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似的性质(解析版) 题型:选择题
如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )
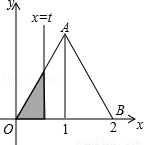
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
如下图,在直角坐标系中,M为![]() 轴上一点,⊙M交
轴上一点,⊙M交![]() 轴于A、B两点,交
轴于A、B两点,交![]() 轴于C、D两点,P为BC上的一个动点,CQ平分∠PCD,A(-1,0),如(1,0)。
轴于C、D两点,P为BC上的一个动点,CQ平分∠PCD,A(-1,0),如(1,0)。
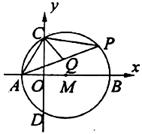
(1)求C点的坐标;
(2)当P点运动时,线段AQ的长度是否改变?若不变,请求其值;若改变请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com