练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．下列等式一定成立的是（　　）
    A．a2×a5=a10B．$\sqrt{a+b}=\sqrt{a}+\sqrt{b}$C．（-a3）4=a12D．$\sqrt{a^2}=a$

    分析 依次根据幂的乘法，算术平方根的运算，幂的乘方，二次根式的化简判断即可．

    解答 解：A、a2×a5=a7≠a10，所以A错误，
    B、$\sqrt{a+b}$不能化简，所以B错误．
    C、（-a3）4=a12，所以C正确，
    D、$\sqrt{{a}^{2}}$=|a|，所以D错误，
    故选C

    点评 此题是二次根式的加减法，主要考查了幂的乘法，算术平方根的运算，幂的乘方，二次根式的化简，熟练运用这些知识点是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    12．计算：16×2-4=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，已知BE=CD，要使△ABE≌△ACD，要添加一个条件是∠B=∠C．（只填一种情况）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

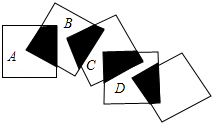    10．将五个边长都为2cm的正方形按如图所示摆放，点A、B、C、D分别是四个正方形的中心，则图中四块阴影面积的和是（　　）cm2．
    A．2cm2B．4cm2C．6cm2D．8cm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．若2（a+3）的值与4互为相反数，则a的值为（　　）
    A．-1B．-$\frac{7}{2}$C．-5D．$\frac{1}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．有一列按一定顺序和规律排列的数：
    第一个数是$\frac{1}{1×2}$；
    第二个数是$\frac{1}{2×3}$；
    第三个数是$\frac{1}{3×4}$；
    …
    对任何正整数n，第n个数与第（n+1）个数的和等于$\frac{2}{n×（n+2）}$．
    （1）经过探究，我们发现：$\frac{1}{1×2}=\frac{1}{1}-\frac{1}{2}$，$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$，$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$，
    设这列数的第5个数为a，那么$a＞\frac{1}{5}-\frac{1}{6}$，$a=\frac{1}{5}-\frac{1}{6}$，$a＜\frac{1}{5}-\frac{1}{6}$，哪个正确？
    请你直接写出正确的结论；
    （2）请你观察第1个数、第2个数、第3个数，猜想这列数的第n个数（即用正整数n表示第n数），并且证明你的猜想满足“第n个数与第（n+1）个数的和等于$\frac{2}{n×（n+2）}$”；
    （3）设M表示$\frac{1}{1^2}$，$\frac{1}{2^2}$，$\frac{1}{3^2}$，…，$\frac{1}{{{{2016}^2}}}$，这2016个数的和，即$M=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+…\frac{1}{{{{2016}^2}}}$，
    求证：$\frac{2016}{2017}＜M＜\frac{4031}{2016}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

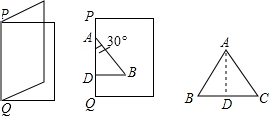    14．如图，欢欢将一张白纸对折，折痕为PQ．以PQ上的线段AD为一条直角边画出直角三角形ABD，使∠DAB=30°，沿折线DBA剪下三角形纸片，将其打开展平，得到△ABC．
    （1）计算∠BAC的度数；
    （2）判断△ABC的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．一个口袋中有 3 个黑球和若干个白球，在不允许将球倒出来数的前提下，小明为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色，…，不断重复上述过程．小明共摸了100次，其中25次摸到黑球．根据上述数据，小明可估计口袋中的白球大约有（　　）
    A．12 个B．15 个C．9 个D．10 个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图，沿AC方向修山路，为了加快施工进度，要在小山的另一边同时施工，从AC上的一点B取∠ABD=145°，BD=500米，∠D=55°，使A、C、E在一条直线上，那么开挖点E与D的距离是（　　）
    A．500sin55°米B．500cos35°米C．500cos55°米D．500tan55°米

    查看答案和解析>>

    同步练习册答案