【题目】如图，已知在RtABC中，∠C=90°，∠A=30°，在直线AC上找点P，使△ABP是等腰三角形，则∠APB的度数为_______________
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目：初中数学 来源： 题型：
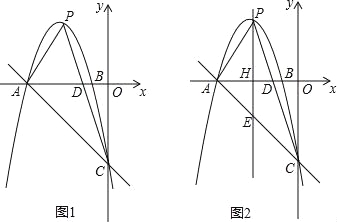
【题目】如图1，抛物线y=ax2﹣6x+c与x轴交于点A（﹣5，0）、B（﹣1，0），与y轴交于点C（0，﹣5），点P是抛物线上的动点，连接PA、PC，PC与x轴交于点D．
（1）求该抛物线所对应的函数解析式；
（2）若点P的坐标为（﹣2，3），请求出此时△APC的面积；
（3）过点P作y轴的平行线交x轴于点H，交直线AC于点E，如图2．
①若∠APE=∠CPE，求证：=；
②△APE能否为等腰三角形？若能，请求出此时点P的坐标；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（10分）如图（1）在ΔABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于点D，BE⊥MN于点E．
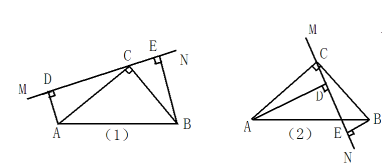
（1）求证：①ΔADC≌ΔCEB ②DE=AD+BE
（2）当直线MN绕点C旋转到图（2）的位置时，DE、AD、BE 有怎样的关系？并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】使用计算器计算各式：6×7= ，66×67= ，666×667= ，6 666×6 667= ．
（1）根据以上结果，你发现了什么规律？
（2）依照你发现的规律，不用计算器，你能直接写出666 666×666 667的结果吗？请你试一试．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列一段文字，然后回答问题．
已知在平面内两点P1（x1，y1）、P2（x2，y2），其两点间的距离P1P2=
，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|．
（1）已知A（2，4）、B（-3，-8），试求A、B两点间的距离；
（2）已知A、B在平行于y轴的直线上，点A的纵坐标为4，点B的纵坐标为-1，试求A、B两点间的距离；
（3）已知一个三角形各顶点坐标为D（1，6）、E（-2，2）、F（4，2），你能判定此三角形的形状吗？说明理由；
（4）平面直角坐标中，在x轴上找一点P，使PD+PF的长度最短，求出点P的坐标以及PD+PF的最短长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了开展阳光体育运动，让学生每天能锻炼一小时，某学校去体育用品商店购买篮球与足球，篮球每只定价100元，足球每只定价50元．体育用品商店向学校提供两种优惠方案：①买一只篮球送一只足球；②篮球和足球都按定价的80%付款．现学校要到该体育用品商店购买篮球30只，足球x只（x>30）．
（1）若该学校按方案①购买，篮球需付款 元，足球需付款 元（用含x的式子表示）；
若该学校按方案②购买，篮球需付款 元，足球需付款 元（用含x的式子表示）；
（2）若x=40，请通过计算说明按方案①、方案②哪种方案购买较为合算？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在某次试验数据整理过程中，某个事件发生的频率情况如表所示．
试验次数 | 10 | 50 | 100 | 200 | 500 | 1000 | 2000 |
事件发生的 | 0.245 | 0.248 | 0.251 | 0.253 | 0.249 | 0.252 | 0.251 |
估计这个事件发生的概率是（精确到0.01）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
