
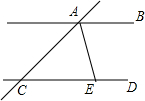
 如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )
如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠DEA=( )| A. | 40° | B. | 110° | C. | 70° | D. | 140° |
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | ${y_2}=\frac{9}{8x}$ | B. | ${y_2}=\frac{1}{2x}$ | C. | ${y_2}=\frac{2}{x}$ | D. | ${y_2}=-\frac{2}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形的内角和是180° | B. | 直径所对的圆周角是100° | ||
| C. | 若x2=4,则x=±2 | D. | 抛物线与x轴有2个交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
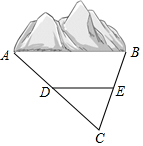 某地需要开辟一条笔直隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使C到A,B两点均可直接到达,测量找到AC和BC的中点D,E,测得DE的长为1 100m,则隧道AB的长度为( )
某地需要开辟一条笔直隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使C到A,B两点均可直接到达,测量找到AC和BC的中点D,E,测得DE的长为1 100m,则隧道AB的长度为( )| A. | 3 300 m | B. | 2 200 m | C. | 1 100 m | D. | 550 m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
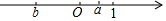 已知实数a、b在数轴上的位置如图所示,则下列等式成立的是( )
已知实数a、b在数轴上的位置如图所示,则下列等式成立的是( )| A. | |a+b|=a+b | B. | |a+b|=a-b | C. | |a+1|=a+1 | D. | |b+1|=b+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的横坐标是( )
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的横坐标是( )| A. | 2 | B. | 2n-1 | C. | 2n | D. | 2n+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com