
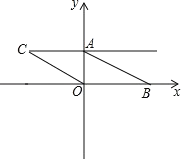
����Ŀ����ƽ��ֱ������ϵ�У�A(a��0)��C(0��c)�����㣺(a+6)2+![]() ��0��������ABCO������ϵ��(��ͼ)����OΪ����ϵ��ԭ�㣮
��0��������ABCO������ϵ��(��ͼ)����OΪ����ϵ��ԭ�㣮
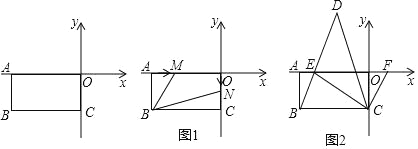
(1)���B�����꣮
(2)��ͼ1������M�ӵ�A��������2����λ/����ٶ������˶�(��������O)����N��ԭ��O��������1����λ/����ٶ������˶�(��������C)����M��N����ͬʱ�������������˶��Ĺ����У��ı���MBNO������Ƿ����仯�������䣬����ֵ�����仯����仯�ķ�Χ��
(3)��ͼ2��EΪx�Ḻ������һ�㣬�ҡ�CBE����CEB��F��x����������һ���㣬��ECF��ƽ����CD��BE���ӳ����ڵ�D���ڵ�F�˶��Ĺ����У���̽����CFE���D��������ϵ����˵������
���𰸡�(1)B(��6����3)��(2)�ı���MBNO��������䣻�Ƕ�ֵ9��(3)��CFE��2��D.
��������
��1����������ɵ�a����6��c����3�������A�㣬C�㣬B�����ꣻ��2����M��Nͬʱ������ʱ��Ϊt����S�ı���MBNO��S������OABC��S��ABM��S��BCN��18��![]() ��2t��3��
��2t��3��![]() ��6����3��t����9����ʱ���أ�������Ƕ�ֵ����ֵΪ9����3�������������ڽǺͶ�������������ǵ��ڲ����ڵ������ڽǵĺͣ������CFE���D��������ϵ��
��6����3��t����9����ʱ���أ�������Ƕ�ֵ����ֵΪ9����3�������������ڽǺͶ�������������ǵ��ڲ����ڵ������ڽǵĺͣ������CFE���D��������ϵ��
�⣺(1)��(a+6)2+![]() ��0��
��0��
��a����6��c����3
��A(��6��0)��C(0����3)
���ı���OABC�Ǿ���
��AO��BC��AB��OC��AB��OC��3��AO��BC��6
��B(��6����3)
(2)�ı���MBNO��������䣮
��M��Nͬʱ������ʱ��Ϊt��
��S�ı���MBNO��S������OABC��S��ABM��S��BCN��18��![]() ��2t��3��
��2t��3��![]() ��6��(3��t)��9����ʱ���أ�
��6��(3��t)��9����ʱ���أ�
�����˶�������������䣮�Ƕ�ֵ9
(3)��CFE��2��D��
�������£���ͼ
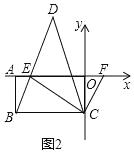
�ߡ�CBE����CEB
���ECB��180����2��BEC
��CDƽ�֡�ECF
���DCE����DCF
��AF��BC
���F��180������DCF����DCE����BCE��180����2��DCE��(180����2��BEC)
���F��2��BEC��2��DCE
�ߡ�BEC����D+��DCE
���F��2(��D+��DCE)��2��DCE
���F��2��D



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����С���ƻ���һ�鳤Ϊ20�ף���12�ľ��γ��������������ഹֱ�ij������·��һ���M�����������Һ�������Ŀ��ȱ�Ϊ3��2�������ಿ���ֻ��ݣ���Ҫʹ�ֻ��ݵ�����ﵽ144��2���������·��Ϊ_____�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
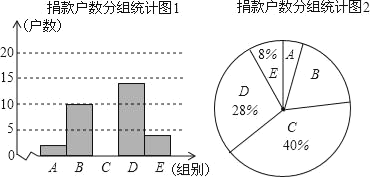
����Ŀ��Ϊ���ø����ʧѧ��ͯ�ط�У��ij������֯���װ��������֡���������������־������е���ͷ���ͳ�ƺ�������������ͼ��ʾ��ͳ��ͼ��ͳ�Ʊ�(ͼ����Ϣ������)����֪A��B��������ı�Ϊ1��5������������Ϣ����������⣮��������ͳ�Ʊ�
��� | ����(x)Ԫ | ���� |
A | 1��x��50 | a |
B | 50��x��100 | 10 |
C | 100��x��150 | �� �� |
D | 150��x��200 | �� �� |
E | x��200 | �� �� |
(1)a���� ����������������������� ����
(2)��ȫ����������ͳ��ͼ1�;�������ͳ�Ʊ�����
(3)����������2000��ס���������������Ϣ������ȫ����������150Ԫ�Ļ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�о���ѧϰС����ѧϰ���θ�ʽ ![]() =|a|֮���о��������ĸ����⣬���д�����ǣ� ��
=|a|֮���о��������ĸ����⣬���д�����ǣ� ��
A.��a��1�������»������ʽa+ ![]() �Ľ��Ϊ2a��1
�Ľ��Ϊ2a��1
B.��a+ ![]() ��ֵ��Ϊ��ֵʱ����ĸa��ȡֵ��Χ��a��1
��ֵ��Ϊ��ֵʱ����ĸa��ȡֵ��Χ��a��1
C.a+ ![]() ��ֵ��a�仯���仯����aȡij����ֵʱ����������ʽ��ֵ����Ϊ
��ֵ��a�仯���仯����aȡij����ֵʱ����������ʽ��ֵ����Ϊ ![]()
D.�� ![]() =��
=�� ![]() ��2 �� ����ĸa��������a��1
��2 �� ����ĸa��������a��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����㣺���Ķ����²��ϣ��������Ӧ������ ��ϣ���ļ���ѧ�Һ��������ġ�������һ���и��������������ε�����������������ġ�����ʽ�������һ�������ε����߳��ֱ�Ϊa��b��c����p= ![]() ���������ε����S=
������������S= ![]() ��
��
�ҹ�������������ѧ���ؾ��أ���������������ε�����������ġ��ؾ��ع�ʽ������б������������һ�������ε����߳��ֱ�Ϊa��b��c���������ε����S= ![]() ��
��
��1����һ�������ε����߳��ֱ���5��6��7������������ε�������� ��
��2����һ�������ε����߳��ֱ��� ![]() ������������ε������
�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
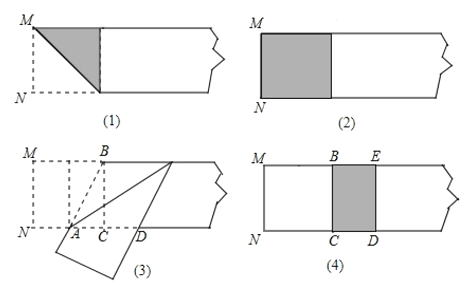
����Ŀ������������ֽ��Ϸ����һ������һ�ž���ֽƬ��һ�ˣ�����ͼ![]() �ķ����۳�һ�������Σ�Ȼ���ֽƬչ�����ڶ�������ͼ
�ķ����۳�һ�������Σ�Ȼ���ֽƬչ�����ڶ�������ͼ![]() ��������������۳�������ȵľ��Σ��ٰ�ֽƬչ�������������۳��ڲ���εĶԽ���
��������������۳�������ȵľ��Σ��ٰ�ֽƬչ�������������۳��ڲ���εĶԽ���![]() ���������۵�ͼ
���������۵�ͼ![]() ����ʾ��
����ʾ��![]() �������IJ�����ͼ
�������IJ�����ͼ![]() �� չƽֽƬ���������õ�
�� չƽֽƬ���������õ�![]() ���۳�
���۳�![]() �������
�������![]() �Ŀ�
�Ŀ�![]() �볤
�볤![]() �ı���__________��
�ı���__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��CD����ABE����CDE�����ǵĽ�ƽ�����ཻ��F��
��1����ͼ1������E=80��������BFD�Ķ�����
��2����ͼ2������ABM=![]() ��ABF����CDM=
��ABF����CDM=![]() ��CDF��д����M����E֮���������ϵ��֤����Ľ��ۣ�
��CDF��д����M����E֮���������ϵ��֤����Ľ��ۣ�
��3������ABM��![]() ��ABF, ��CDM��
��ABF, ��CDM��![]() ��CDF, ����E��m��,ֱ���ú���n��m���Ĵ���ʽд����M�� (��д����)
��CDF, ����E��m��,ֱ���ú���n��m���Ĵ���ʽд����M�� (��д����)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵ�У��� A��0��m������ B��n��0����D��2m��n������ m��n ���㣨m��2��2+![]() =0�����߶�AB����ƽ�ƣ�ʹ��B��� O�غϣ���C���A��Ӧ��
=0�����߶�AB����ƽ�ƣ�ʹ��B��� O�غϣ���C���A��Ӧ��
��1�����C��D�����ꣻ
��2������CD������P�ӵ�O��������ÿ��1����λ���ٶȣ�������OB�����˶������P�˶�ʱ��Ϊt�룬�Ƿ����ijһʱ�̣�ʹ SPCD=4SAOB�������ڣ������tֵ����д��P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� ABCD�У�CD=2AD��BE��AD�ڵ�E��FΪDC���е㣬����EF��BF�����н��ۣ��١�ABC=2��ABF����EF=BF����S�ı���DEBC=2S��EFB���ܡ�CFE=3��DEF,������ȷ���۵ĸ������У� ��.

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com