
【题目】如图,点![]() 在
在![]() 直径
直径![]() 的延长线上,点
的延长线上,点![]() 在
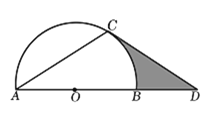
在![]() 上,且AC=CD,∠ACD=120°.
上,且AC=CD,∠ACD=120°.
(1)求证: ![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)2![]()
![]() .
.
【解析】试题分析:(1)连接OC.只需证明∠OCD=90°.根据等腰三角形的性质即可证明;
(2)阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积.
试题解析:(1)证明:连接OC.

∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=180°-∠A-∠D-∠2=90°.即OC⊥CD,
∴CD是⊙O的切线.
(2)∵∠A=30°,
∴∠1=2∠A=60°.
∴S扇形BOC=![]() .
.
在Rt△OCD中,
∵![]() =tan60°,
=tan60°,
∴CD=2![]() .
.
∴SRt△OCD=![]() OC×CD=
OC×CD=![]() ×2×2
×2×2![]() =2
=2![]() .
.
∴图中阴影部分的面积为:2![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】在一条直线上依次有A、B、C三个港口,A、B两港相距30千米,B、C两港相距90千米.甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.甲0.5小时到达B港,此时两船相距15千米.
求:(1)甲船何时追上乙,此时乙离C港多远?
(2)何时甲乙两船相距10千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作如图,∠△ABC是直角三角形,∠ACB=90,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作∠BAC的平分线,交BC于点0
②以点0为圆心,OC为半径作圆.综合运用在你所作的图中,
(1)直线AB与⊙0的位置关系是
(2)证明:BA·BD=BC·BO;
(3)若AC=5,BC=12,求⊙0的半径

查看答案和解析>>
科目:初中数学 来源: 题型:
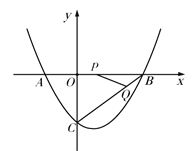
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)请直接写出A、B、C三点的坐标:
A B C
(2)点P从点A出发,在线段AB上以每秒3个单位长度的速度向点B运动,同时点Q 从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动.其中一个点到达终点时,另一个点也停止运动.设运动的时间为t(秒),
① 当t为何值时,BP=BQ?
② 是否存在某一时刻t,使△BPQ是直角三角形?若存在,请求出所有符合条件的t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
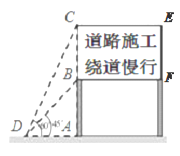
【题目】我市在高架快速公路施工期间,交管部门在施工路段设立了矩形路况警示牌BCEF(如图所示),已知立杆AB的高度是3米,从侧面D点测到路况警示牌顶端C点和底端B点的仰角分别是60°和45°,求路况警示牌宽BC的值(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com