
【题目】(感知)如图1,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,易知
,易知![]() ,得到点
,得到点![]() 的坐标为
的坐标为![]() .
.
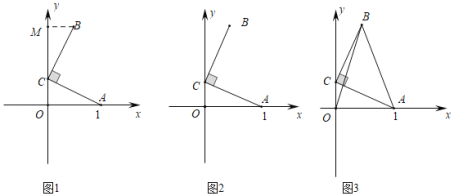
(探究)如图2,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() .
.
(1)求点![]() 的坐标.(用含
的坐标.(用含![]() 的代数式表示)
的代数式表示)
(2)求出BC所在直线的函数表达式.
(拓展)如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,将线段
轴上,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() ,连结
,连结![]() 、
、![]() ,则
,则![]() 的最小值为_______.
的最小值为_______.
【答案】【探究】(1)点![]() 坐标为
坐标为![]() ;(2)
;(2)![]() ;【拓展】
;【拓展】![]() .
.
【解析】
探究:(1)证明△AOC≌△CMB(AAS),即可求解;
(2)根据点B的坐标为(m,m+1),点![]() 坐标
坐标![]() ,即可求解;
,即可求解;
拓展:BO+BA=![]() ,BO+BA的值,相当于求点P(m,m)到点M(1,-1)和点N(0,-1)的最小值,即可求解.
,BO+BA的值,相当于求点P(m,m)到点M(1,-1)和点N(0,-1)的最小值,即可求解.
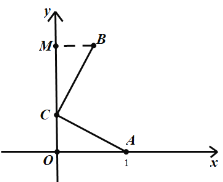
解:探究:(1)过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .
.
![]() ,
,
![]() .
.
![]() 线段
线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() 点
点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ,
,
![]() 点
点![]() 坐标为
坐标为![]()
(2)∵点B的坐标为(m,m+1),点C为(0,m),
设直线BC为:y=kx+b,
![]() ,解得:
,解得: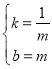 ,
,
∴![]() ;
;
则BC所在的直线为:![]() ;
;
拓展:如图作BH⊥OH于H.
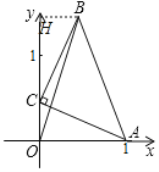
设点C的坐标为(0,m),
由(1)知:OC=HB=m,OA=HC=1,
则点B(m,1+m),
则:BO+BA=![]() ,
,
BO+BA的值,相当于求点P(m,m)到点M(1,-1)和点N(0,-1)的最小值,
相当于在直线y=x上寻找一点P(m,m),使得点P到M(0,-1),到N(1,-1)的距离和最小,
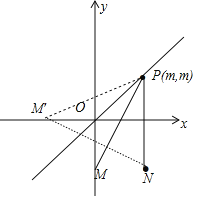
作M关于直线y=x的对称点M′(-1,0),
易知PM+PN=PM′+PN≥NM′,
M′N=![]() ,
,
故:BO+BA的最小值为![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
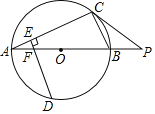
【题目】如图,AB为⊙O的直径,点P在AB的延长线上,点C在⊙O上,且PC2=PBPA.
(1)求证:PC是⊙O的切线;
(2)已知PC=20,PB=10,点D是![]() 的中点,DE⊥AC,垂足为E,DE交AB于点F,求EF的长.
的中点,DE⊥AC,垂足为E,DE交AB于点F,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,等边三角形![]() 的边长为2,
的边长为2,![]() 是
是![]() 边上的任一点(与
边上的任一点(与![]() 不重合),设
不重合),设![]() ,连接
,连接![]() ,以
,以![]() 为边向两侧作等边三角形
为边向两侧作等边三角形![]() 和等边三角形
和等边三角形![]() ,分别与边
,分别与边![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)求四边形![]() 与△ABC重叠部分的面积
与△ABC重叠部分的面积![]() 与
与![]() 之间的函数关系式及
之间的函数关系式及![]() 的最小值;
的最小值;
(3)如图②,连接![]() ,分别与边
,分别与边![]() 交于点
交于点![]() .当
.当![]() 为何值时,
为何值时,![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,且与抛物线交于
,且与抛物线交于![]() ,
,![]() 两点,
两点,![]() 为抛物线上一动点(不与
为抛物线上一动点(不与![]() ,
,![]() 重合).
重合).
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 下方时,过点
下方时,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值.
的最大值.
(3)设![]() 为直线
为直线![]() 上的点,以
上的点,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否构成平行四边形?若能,求出点
为顶点的四边形能否构成平行四边形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
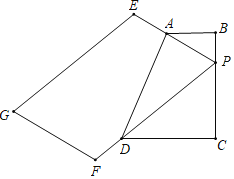
【题目】在四边形ABCD中,AB∥CD,BC⊥CD,AB=2,CD=3,在BC上取点P(P与B、C不重合)连接PA延长至E,使PA=2AE,连接PD并延长至F,使PD=3FD,以PE、PF为边作平行四边形,另一个顶点为G,则PG长度的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
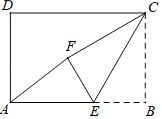
【题目】如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是_____(写出所有正确结论的序号)
①当E为线段AB中点时,AF∥CE;
②当E为线段AB中点时,AF=![]() ;
;
③当A、F、C三点共线时,AE=![]() ;
;
④当A、F、C三点共线时,△CEF≌△AEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形 ABCD中,AB=AD,∠BAD=60°,边BC绕点B顺时针旋转120°得到BE,边DC绕点D逆时针旋转120°得到DF,四边形ABEG和四边形ADFH为平行四边形.
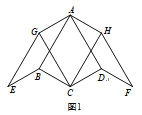
(1)如图1,若BC=CD,∠BCD=120°,则∠GCH=_______°;
(2)如图2,若BC≠CD,探究∠GCH的大小是否发生变化,并证明你的结论;
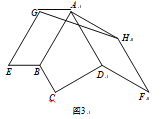
(3)如图3,若∠BCD=∠ADC=90°,AB=![]() 请直接写出△AGH的周长.
请直接写出△AGH的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应任务:
黄金分割
天文学家开普勒把黄金分割称为神圣分割,并指出毕达哥拉斯定理(勾股定理)和黄金分割是几何中的双宝,前者好比黄金,后者堪称珠宝,历史上最早正式在书中使用“黄金分割”这个名称的是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割指把一条线段分为两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比,该比值为![]() .用下面的方法(如图①)就可以作出已知线段
.用下面的方法(如图①)就可以作出已知线段![]() 的黄金分割点
的黄金分割点![]() :
:

①以线段![]() 为边作正方形
为边作正方形![]() ,
,
②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
③延长![]() 到
到![]() ,使
,使![]() ,
,
④以线段![]() 为边作正方形
为边作正方形![]() ,点
,点![]() 就是线段
就是线段![]() 的黄金分割点.
的黄金分割点.
以下是证明点![]() 就是线段
就是线段![]() 的黄金分割点的部分过程:
的黄金分割点的部分过程:
证明:设正方形![]() 的边长为1,则
的边长为1,则![]() ,
,
![]() 为
为![]() 中点,
中点,
![]() ,
,
![]() 在
在![]() 中,
中,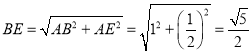 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…
任务:
(1)补全题中的证明过程;
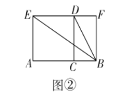
(2)如图②,点![]() 为线段
为线段![]() 的黄金分割点,分别以
的黄金分割点,分别以![]() 为边在线段
为边在线段![]() 同侧作正方形
同侧作正方形![]() 和矩形
和矩形![]() ,连接
,连接![]() .求证:
.求证:![]() ;
;
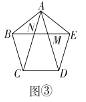
(3)如图③,在正五边形![]() 中,对角线
中,对角线![]() 与
与![]() 分别交于点
分别交于点![]() 求证:点
求证:点![]() 是
是![]() 的黄金分割点.
的黄金分割点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com