
【题目】如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)当t= ![]() 秒时,则OP= , S△ABP=;
秒时,则OP= , S△ABP=;
(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQBP=3.
【答案】
(1)1;![]()
(2)
解:当△ABP是直角三角形时,
①若∠A=90°.
∵∠BOC=60°且∠BOC>∠A,
∴∠A≠90°,故此种情形不存在;
②若∠B=90°,如答图2所示:

∵∠BOC=60°,
∴∠BPO=30°,
∴OP=2OB=2,又OP=2t,
∴t=1;
③若∠APB=90°,如答图3所示:

过点P作PD⊥AB于点D,则OD=OPsin30°=t,PD=OPsin60°= ![]() t,
t,
∴AD=OA+OD=2+t,BD=OB﹣OD=1﹣t.
在Rt△ABP中,由勾股定理得:PA2+PB2=AB2
∴(AD2+PD2)+(BD2+PD2)=AB2,
即[(2+t)2+( ![]() t)2]+[(1﹣t)2+(
t)2]+[(1﹣t)2+( ![]() t)2]=32
t)2]=32
解方程得:t= ![]() 或t=
或t= ![]() (负值舍去),
(负值舍去),
∴t= ![]() .
.
综上所述,当△ABP是直角三角形时,t=1或t= ![]()
(3)
证明:如答图4,过点O作OE∥AP,交PB于点E,

则有 ![]() ,
,
∴PE= ![]() PB.
PB.
∵AP=AB,
∴∠APB=∠B,
∵OE∥AP,
∴∠OEB=∠APB,
∴∠OEB=∠B,
∴OE=OB=1,∠3+∠B=180°.
∵AQ∥PB,
∴∠OAQ+∠B=180°,
∴∠OAQ=∠3;
∵∠AOP=∠1+∠QOP=∠2+∠B,∠QOP=∠B,
∴∠1=∠2;
∴△OAQ∽△PEO,
∴ ![]() ,即
,即 ![]() ,
,
化简得:AQPB=3
【解析】(1)解:当t= ![]() 秒时,OP=2t=2×
秒时,OP=2t=2× ![]() =1.
=1.
如答图1,过点P作PD⊥AB于点D.
在Rt△POD中,PD=OPsin60°=1× ![]() =
= ![]() ,
,
∴S△ABP= ![]() ABPD=
ABPD= ![]() ×(2+1)×
×(2+1)× ![]() =
= ![]() .
.
(1)如答图1所示,作辅助线,利用三角函数或勾股定理求解;(2)当△ABP是直角三角形时,有三种情形,需要分类讨论;(3)如答图4所示,作辅助线,构造一对相似三角形△OAQ∽△PBO,利用相似关系证明结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3 ![]() ,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆. 
(1)求BC的长;
(2)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
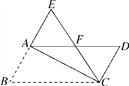
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表: 身高情况分组表(单位:cm)
组别 | 身高 |
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在组,中位数在组;
(2)样本中,女生身高在E组的人数有人;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.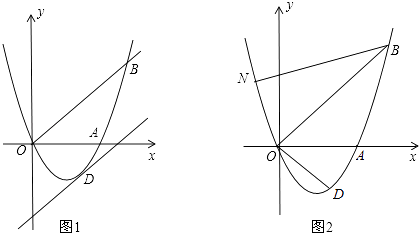
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).
查看答案和解析>>
科目:初中数学 来源: 题型:
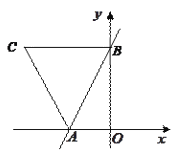
【题目】如图,已知一次函数![]() 的图像与x轴、
的图像与x轴、![]() 轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
(1)求点A、B、C的坐标;
(2)求直线AC的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com