
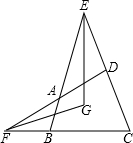
 如图,在四边形ABCD中,点E和点F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠CFD,且∠ADC=60°,∠ABC=80°,则∠EGF的度数是110°.
如图,在四边形ABCD中,点E和点F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠CFD,且∠ADC=60°,∠ABC=80°,则∠EGF的度数是110°. 分析 连接EF,根据三角形内角和等于180°及三角形角平分线的性质,即可得出∠EGF=$\frac{1}{2}$(360°-∠ABC-∠ADC),代入∠ADC=60°、∠ABC=80°,即可求出∠EGF的度数.
解答 解:连接EF,如图所示.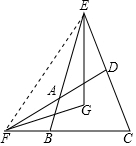
∠EGF=180°-(∠GFE+∠GEF),
=180°-(∠CFE-∠CFG+∠CEF-∠CEG),
=180°-(∠CFE+∠CEF)+(∠CFG+∠CEG),
=180°-(180°-∠C)+( $\frac{1}{2}$∠CFD+$\frac{1}{2}$∠CEB),
=∠C+$\frac{1}{2}$(∠CFD+∠CEB),
=∠C+$\frac{1}{2}$(180°-∠C-∠CDA+180°-∠C-∠CBA),
=$\frac{1}{2}$(360°-∠ABC-∠ADC),
=110°.
故答案为:110°.
点评 本题考查了三角形内角和定理、角平分线的性质以及多边形的内角与外角,根据角与角之间的关系找出∠EGF=$\frac{1}{2}$(360°-∠ABC-∠ADC)是解题的关键.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
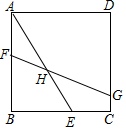 如图,在正方形ABCD中,AB=3,E为BC上一点,连接AE,H为AE的中点,过点H作直线FG交AB于F,交CD于G,若∠AHF=30°,AE=FG,则CG的长度为2-$\sqrt{3}$.
如图,在正方形ABCD中,AB=3,E为BC上一点,连接AE,H为AE的中点,过点H作直线FG交AB于F,交CD于G,若∠AHF=30°,AE=FG,则CG的长度为2-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD内部画△ADP,使PA=PD,若∠APD=30°,点P在∠ABC的平分线上,则$\frac{AB}{BC}$的值是( )
如图,在矩形ABCD内部画△ADP,使PA=PD,若∠APD=30°,点P在∠ABC的平分线上,则$\frac{AB}{BC}$的值是( )| A. | $\frac{3+\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}+3\sqrt{2}}{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{5\sqrt{2}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,扇形和正方形ABCD,半径与AB重合,扇形的弧长和AB相等,已知AB=20,扇形沿着正方形翻滚到首次与起始位置相同,则点O经过的路径长为80+80π.
如图,扇形和正方形ABCD,半径与AB重合,扇形的弧长和AB相等,已知AB=20,扇形沿着正方形翻滚到首次与起始位置相同,则点O经过的路径长为80+80π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | f1+f2+…+fk | B. | x1+x2+…+xk | C. | 1+2+…+k | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
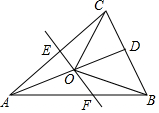 如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是( )
如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com