
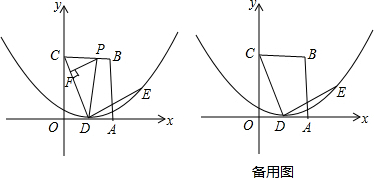
分析 (1)过点E作EG⊥x轴于G点.先证明△ODC≌△GED,从而得到∴EG=OD=2,DG=OC=4,故此可得到点E的坐标,然后设抛物线的解析式为y=a(x-2)2,最后将点E的坐标代入抛物线的解析式可求得a的值;
(2)①当△DFP∽△COD,则∠PDF=∠DCO,依据平行线的判定定理可知PD∥OC,然后可证明四边形PDOC是矩形,则PC=OD=2,故此可求得t的值;②当△PFD∽△COD,可证明∠PCF=∠PDF,则PC=PD.设P(t,4),则CP=t,DP=$\sqrt{(t-2)^{2}+{4}^{2}}$,然后由PC=PD列方程求解即可;
(3)当点Q在点P的左侧时,设点P的坐标为(t,0),点Q的坐标为(x,y),依据平分四边形对角线互相平分的性质和线段的中点坐标公式可求得y=2,x=t-4,从而得到点Q的坐标,然后将点Q的坐标代入抛物线的解析式求解即可;当点Q在点P的右侧时,同理可求得点Q的坐标.
解答 解:(1)如图1,过点E作EG⊥x轴于G点.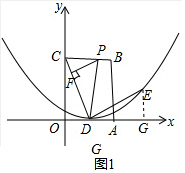
∵四边形OABC是边长为4的正方形,D是OA的中点,
∴OA=OC=4,OD=2,∠AOC=∠DGE=90°.
∵∠CDE=90°,
∴∠ODC+∠GDE=90°.
∵∠ODC+∠OCD=90°,
∴∠OCD=∠GDE.
在△OCD和△GED中$\left\{\begin{array}{l}{∠COD=∠DGE}\\{∠OCD=∠GDE}\\{DC=DE}\end{array}\right.$,
∴△ODC≌△GED (AAS),
∴EG=OD=2,DG=OC=4.
∴点E的坐标为(6,2).
∵点D为抛物线的顶点,
∴可设抛物线的解析式为y=a(x-2)2,
将E点的坐标代入解析式,得2=a(6-2)2,
解得a=$\frac{1}{8}$,
抛物线的解析式为y=$\frac{1}{8}$(x-2)2;
(2)①若△DFP∽△COD,则∠PDF=∠DCO,
∴PD∥OC,
∴∠PDO=∠OCP=∠AOC=90°,
∴四边形PDOC是矩形,
∴PC=OD=2,
∴t=2;
②当△PFD∽△COD,则∠DPF=∠DCO,.
∴∠PCF=90°-∠DCO=90°-∠DPF=∠PDF.
∴PC=PD.
设P(t,4),则CP=t,DP=$\sqrt{(t-2)^{2}+{4}^{2}}$.
∴t2=(t-2)2+16,解得t=5.
综上所述:t=2或t=5时,以点P,F,D为顶点的三角形与△COD相似;
(3)如图2所示: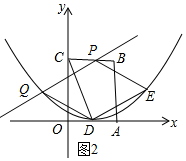
设点P的坐标为(t,0),点Q的坐标为(x,y).
∵四边形DEPQ为平行四边形,
∴PD与QE相互平分.
∴依据中点坐标公式可知:$\frac{6+x}{2}$=$\frac{t+2}{2}$,$\frac{2+y}{2}=\frac{0+4}{2}$.
∴y=2,x=t-4.
将点Q的坐标代入抛物线的解析式得:$\frac{1}{8}$(t-6)2=2,解得:t=2或t=10(舍去).
∴x=-2,y=2,.
∴点Q的坐标为(-2,2).
如图3所示:
∵PE和DQ为平行四边形的对角线,
∴PE与QD互相平分.
∴$\frac{x+2}{2}$=$\frac{t+6}{2}$,$\frac{y+0}{2}$=$\frac{4+2}{2}$.
∴y=6,x=t+4.
将点Q的坐标代入抛物线的解析式得:$\frac{1}{8}$(t+2)2=6,解得:t=4$\sqrt{3}$-2或t=-4$\sqrt{3}$-2(舍去).
∴x=4$\sqrt{3}$+2.
∴点Q的坐标为(4$\sqrt{3}$+2,6).
∴点Q的坐标为(-2,2)或(4$\sqrt{3}$+2,6).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了全等三角形的性质和判定、相似三角形的性质、平行四边形的性质、待定系数法求二次函数的解析式,依据全等三角形的性质得到点E的坐标是解答问题(1)的关键;分类讨论是解答问题(2)的关键;依据平行四边形的性质得到点Q的坐标(用含t的式子表示)是解答问题(3)的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 
| ||||||||||||||||||||||||||||||
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
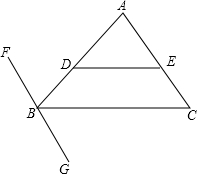 如图,点D、E分别在△ABC的边AB、AC上,且DE∥BC,过点B作直线FG,使∠CBG=∠AED,请判断FG与AC是否平行?并说明理由.
如图,点D、E分别在△ABC的边AB、AC上,且DE∥BC,过点B作直线FG,使∠CBG=∠AED,请判断FG与AC是否平行?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
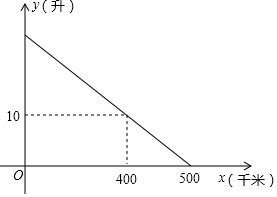 已知某汽车装满油后邮箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶450千米,就应该停车加油.
已知某汽车装满油后邮箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶450千米,就应该停车加油.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
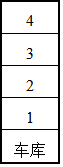 小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯.
小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A 乙没有抽到自己带来的礼物 | B 乙恰好抽到自己带来的礼物 |
| C 乙抽到一件礼物 | D 只有乙抽到自己带来的礼物 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象与一次函数y=k2x+b的图象交于A(1,6),B(m,2)两点.
如图,反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象与一次函数y=k2x+b的图象交于A(1,6),B(m,2)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com