
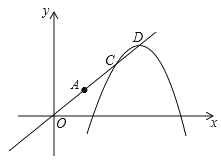
【题目】已知抛物线y=﹣x2+mx+m﹣2的顶点为A,且经过点(3,﹣3).
(1)求抛物线的解析式及顶点A的坐标;
(2)将原抛物线沿射线OA方向进行平移得到新的抛物线,新抛物线与射线OA交于C,D两点,如图,请问:在抛物线平移的过程中,线段CD的长度是否为定值?若是,请求出这个定值;若不是,请说明理由.
【答案】(1)y=﹣x2+2x,顶点A的坐标是(1,1);(2)CD长为定值![]() .
.
【解析】
(1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)根据平移规律,可设出新抛物线解析式,联立抛物线与直线OA,可得C、D点的横坐标,根据勾股定理,可得答案.
解:(1)把(3,﹣3)代入y=﹣x2+mx+m-2得:﹣3=﹣32+3m+m-2,
解得m=2,
∴y=﹣x2+2x,
∴y=﹣x2+2x=﹣(x-1)2+1,
∴顶点A的坐标是(1,1);
(2)易得直线OA的解析式为y=x,
平移后抛物线顶点在直线OA上,设平移后顶点为(a,a),
∴可设新的抛物线解析式为y=﹣(x﹣a)2+a,
联立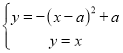
解得:x1=a,x2=a﹣1,
∴C(a-1,a-1),D(a,a),
即C、D两点间的横坐标的差为1,纵坐标的差也为1,
∴CD=![]()
∴CD长为定值![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在研究二次函数及其图像性质的问题时,发现了两个重要结论:
①抛物线 y = ax 2 2x + 3(a ≠0) ,不论 a 为何值时,它的顶点都在某条直线上;
②抛物线 y = ax 2 2x + 3(a ≠0),其顶点的横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() 得到A点,若把顶点的横坐标增加
得到A点,若把顶点的横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() ,得到B点,则A,B两点一定在抛物线y = ax 2 2x + 3上.
,得到B点,则A,B两点一定在抛物线y = ax 2 2x + 3上.
(1)请你帮忙求出抛物线 y = ax 2 2x + 3的顶点所在直线的解析式,并证明结论②是正确的;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗,并说明理由;
(3)你能把结论①或②(选择其中之一)推广到一般情况吗,请用数学语言表述你的成 果,并给予严格的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
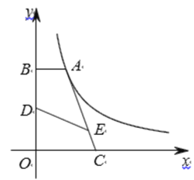
【题目】如图,点![]() 在双曲线
在双曲线![]() 的第一图像的那一支上,
的第一图像的那一支上,![]() 垂直于
垂直于![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,点
,点![]() 为
为![]() 的中点,若
的中点,若![]() 面积为3,则
面积为3,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与轴负半轴交于点
的左侧),与轴负半轴交于点![]() ,若
,若![]() .
.
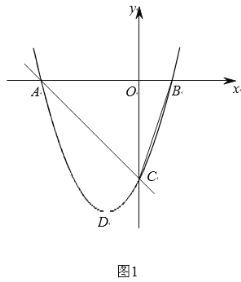
(1)求抛物线的解析式;
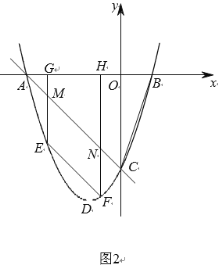
(2)如图2,![]() 是第三象限内抛物线上的动点,过点
是第三象限内抛物线上的动点,过点![]() 交抛物线于点
交抛物线于点![]() ,过
,过![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,当四边形
,当四边形![]() 的周长最大值时,求点
的周长最大值时,求点![]() 的横坐标;
的横坐标;
(3)在![]() 轴下方的抛物线上是否存在一点
轴下方的抛物线上是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形被对角线分成面积相等的两部分.如果存在,求点
为顶点的四边形被对角线分成面积相等的两部分.如果存在,求点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
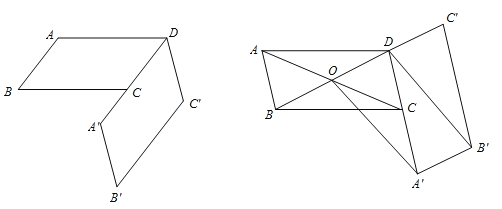
【题目】如图,已知ABCD,AB=m,AD=n,将ABCD绕点D逆时针旋转,得到A’B’CD,点A’在CD延长线上.
(1)若n=4,当B’A’所在直线恰好经过点A时,求点A运动到A’所经过的路径的长度;
(2)连接AC、BD相交于点O,连接OA’、DB’,当四边形OA’B’D为平行四边形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在某条公路上有A,B,C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,又以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图2所示.
(1)当汽车在A,B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)当汽车的行驶路程为360千米时,求此时的行驶时间x的值;
(3)若汽车在某一段路程内行驶了90千米用时50分钟,求行驶完这段路程时x的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com