
【题目】如图1,在菱形ABCD中,![]() ,点E,F分别是AC,AB上的点,且
,点E,F分别是AC,AB上的点,且![]() ,猜想:
,猜想:
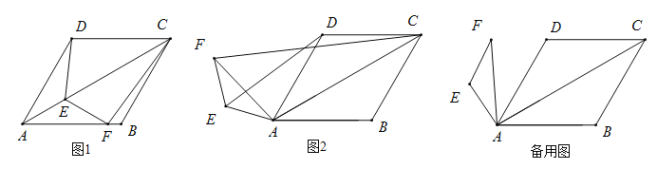
①![]() 的值是_______;
的值是_______;
②直线DE与直线CF所成的角中较小的角的度数是_______.
(2)类比探究:如图2,将绕![]() 点A逆时针旋转,在旋转的过程中,(1)中结论是否成立,就图2的情形说明理由.
点A逆时针旋转,在旋转的过程中,(1)中结论是否成立,就图2的情形说明理由.
(3)拓展延伸:
在![]() 绕点A旋转的过程中,当
绕点A旋转的过程中,当![]() 三点共线时,请直接写出CF的长.
三点共线时,请直接写出CF的长.
【答案】(1)①![]() ;②30度;(2)成立,理由见解析;(3)
;②30度;(2)成立,理由见解析;(3)![]() 或
或![]() ,理由见解析.
,理由见解析.
【解析】
①由![]() 得
得![]() ;
;
②延长DE、CF交于K,由![]() 得
得![]() ,再由
,再由![]() 可得
可得![]()
(2)连接BD交AC于点G, 先证明![]() 可得
可得![]() ,再利用“8”字型可得
,再利用“8”字型可得![]() ;
;
(3)过点A作![]() ,交直线DE于M,再结合(2)中相似分类讨论即可;
,交直线DE于M,再结合(2)中相似分类讨论即可;
(1)①∵菱形ABCD中,![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]() ;
;
②如解题图1,延长DE、CF交于K,
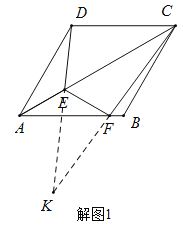
∵![]()
∴![]() ,
,
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
(2)成立,理由如下
如解题图2,连接BD交AC于点G,

∵四边形ABCD是菱形,
∴![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
即直线DE与CF夹角所成的较小角的度数是30度
(3)![]() 或
或![]()
理由如下:
(1)过点A作![]() ,交直线DE于M,如解题图3:
,交直线DE于M,如解题图3:
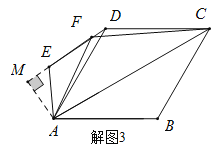
当D,E,F三点共线时![]()
![]() ,
,
![]()
由(2)得![]() ,
,
(2)如解题图4,过点A作![]() ,
,
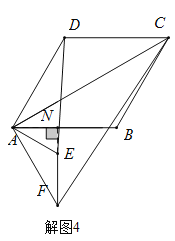
当D,E,F三点共线时![]()
![]() ,
,
![]()
由(2)得![]()


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
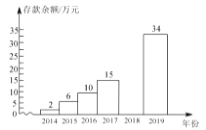
【题目】小李2014年参加工作,每年年底都把本年度收入减去支出后的余额存入银行(存款利息记入收入),2014年底到2019年底,小李的银行存款余额变化情况如下表所示:(单位:万元)
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
收入 | 3 | 8 | 9 |
| 14 | 18 |
支出 | 1 | 4 | 5 | 6 |
| 6 |
存款余额 | 2 | 6 | 10 | 15 |
| 34 |
(1)表格中![]() ________;
________;
(2)请把下面的条形统计图补充完整:(画图后标注相应的数据)
(3)请问小李在哪一年的支出最多?支出了多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动,甲公司共捐款100000元,公司共捐款140000元.下面是甲、乙两公司员工的一段对话:
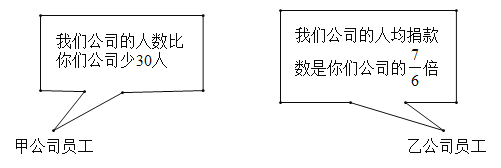
(1)甲、乙两公司各有多少人?
(2)现甲、乙两公司共同使用这笔捐款购买![]() 、
、![]() 两种防疫物资,
两种防疫物资,![]() 种防疫物资每箱15000元,
种防疫物资每箱15000元,![]() 种防疫物资每箱12000元.若购买
种防疫物资每箱12000元.若购买![]() 种防疫物资不少于10箱,并恰好将捐款用完,有几种购买方案?请设计出来(注:
种防疫物资不少于10箱,并恰好将捐款用完,有几种购买方案?请设计出来(注:![]() 、
、![]() 两种防疫物资均需购买,并按整箱配送).
两种防疫物资均需购买,并按整箱配送).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,在公安部交通管理局部署下,全国各地交警都在大力开展|一盔一带安全守护行动,为了解市民对骑电动车戴头盔的赞同情况,某课题小组随机调查了部分市民,并根据调查结果绘制了尚不完整的统计图.
根据以上统计图回答一下问题:
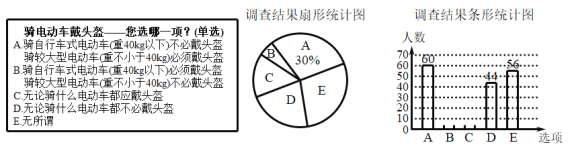
(1)这次调查的市民共_______人;
(2)若选择![]() 的人数是选择
的人数是选择![]() 的人数的3倍,则扇形统计图中,扇形
的人数的3倍,则扇形统计图中,扇形![]() 的圆心角度数是______;
的圆心角度数是______;
(3)补全条形统计图;
(4)若该市约有80万人,请估计安全意识淡薄(选择D或E)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了响应市政府号召,在“创文创卫”活动周中,设置了“![]() :文明礼仪;
:文明礼仪;![]() :环境保护;
:环境保护;![]() ;卫生保洁;
;卫生保洁;![]() :垃圾分类 ”四个主题,每个学生选一个主题参与;为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
:垃圾分类 ”四个主题,每个学生选一个主题参与;为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
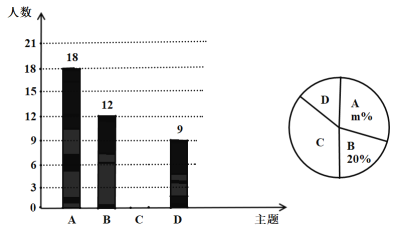
⑴.本次调查的学生人数是 人,![]() = ;
= ;
⑵.请补全条形统计图;
⑶.学校要求每位同学从星期一至星期五选择两天参加活动,如果小张同学随机选择连续两天,其中有一天是星期一的概率是 ;小李同学星期五要参加市演讲比赛,他在其余四天中随机选择两天,其中一天是星期三的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
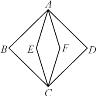
【题目】定义:如图,若菱形AECF与正方形ABCD两个顶点A,C重合,另外两个顶点E,F在正方形ABCD的内部,则称菱形AECF为正方形ABCD的内含菱形.
若正方形的周长为16,其内含菱形边长是整数,则内含菱形的周长为________;
若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售![]() ,
,![]() 两种商品,售出2件
两种商品,售出2件![]() 种商品和3件
种商品和3件![]() 种商品所得利润为700元;售出3件
种商品所得利润为700元;售出3件![]() 种商品和5件
种商品和5件![]() 种商品所得利润为1100元.
种商品所得利润为1100元.
(1)求每件![]() 种商品和每件
种商品和每件![]() 种商品售出后所得利润分别为多少元;
种商品售出后所得利润分别为多少元;
(2)由于需求量大,![]() ,
,![]() 两种商品很快售完,商场决定再一次购进
两种商品很快售完,商场决定再一次购进![]() ,
,![]() 两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么此商场至少需购进多少件
两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么此商场至少需购进多少件![]() 种商品.
种商品.
查看答案和解析>>
科目:初中数学 来源: 题型:
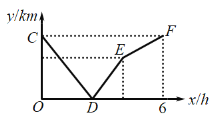
【题目】A,B两地相距240 km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止,在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止,两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线![]() 所示.其中点C的坐标是
所示.其中点C的坐标是![]() ,点D的坐标是
,点D的坐标是![]() ,则点E的坐标是__________.
,则点E的坐标是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com