
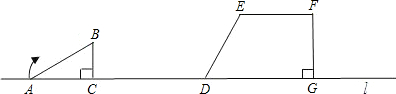
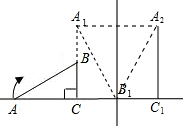
���� ��1��������ת�Ķ���õ�CB��=CB����ֱ��������ABC�У��������Ǻ����Ϳ������BC�ij�����CB��ij����Ϳ������AB1�ij��ȣ�
��2���ı���A2B1DE�����Σ�����֤��A2B��DEƽ������ȣ��õ��ı���A2B1DE��ƽ���ı��Σ���A2B1=B1D=4������ƽ���ı���A2B1DE�����Σ�
��3��y���ڡ�ABC�����һ��ʱ�����������һ���ǵ�A3B2��DE�ཻʱ������2��x��4ʱ������A3B2��DE���õ����غϲ��ֵ����������A3B2C2���ƣ�������ıȵ������Ʊȣ��Ϳ��������ֱ��L���غϲ��ֵij��ȣ��õ�C1C2�ij��ȣ��Ӷ����x��ֵ������һ������ǵ�A3B2��FG�ཻʱ��ͬ�����������������ƾͿ������C1C2�ij��ȣ��Ӷ����x��ֵ��
���  �⣺��1���ڡ�ABC�У�����֪�ã�BC=2cm��AC=AB��cos30��=2$\sqrt{3}$cm��
�⣺��1���ڡ�ABC�У�����֪�ã�BC=2cm��AC=AB��cos30��=2$\sqrt{3}$cm��
��AB1=AC+CB1=AC+CB=��2$\sqrt{3}$+2��cm��
��2���ı���A2B1DE���Σ�
�������£��ߡ�C=90�㣬��A=30�㣬AB=4cm��
��BC=$\frac{1}{2}$AB=$\frac{1}{2}$��4=2cm��
�ߡ�EDG=60�㣬��A2B1C1=��A1B1C=��ABC=60�㣬
��A2B1��DE��
�֡�A2B1=A1B1=AB=4cm��DE=4cm��
��A2B1=DE��
���ı���A2B1DE��ƽ���ı��Σ�
�֡�A2B1=AB=4cm��
B1D=CD-B1C=6-2=4cm��
��A2B1=B1D=4cm��
��ƽ���ı���A2B1DE�����Σ�
��3���������֪��
S��ABC=$\frac{1}{2}$��2��2$\sqrt{3}$=2$\sqrt{3}$cm2��
�ٵ�0��x��2��x��10ʱ��y=0��
��ʱ�ص����ֵ����������ڡ�ABC�������һ�룻
�ڵ�2��x��4ʱ��ֱ�DZ�B2C2��ֱ�����ε��µױ�DG�ص��ij���ΪDC2=C1C2-DC1=��x-2��cm��
��y=$\frac{1}{2}$��x-2��$\sqrt{3}$��x-2��=$\frac{\sqrt{3}}{2}$��x-2��2��
��y=$\frac{1}{2}$S��ABC=$\sqrt{3}$ʱ����$\frac{\sqrt{3}}{2}$��x-2��2=$\sqrt{3}$�����x=2-$\sqrt{2}$���ᣩ��x=2+$\sqrt{2}$��
���Ե�x=��2+$\sqrt{2}$��cmʱ���ص����ֵ�������ڡ�ABC�������һ�룻
�۵�4cm��x��8cmʱ����A3B2C2��ȫ��ֱ�������ص�����y=2$\sqrt{3}$cm2��
�ܵ�8cm��x��10cmʱ��B2G=B2C2-GC2=2-��x-8��=��10-x��cm��
��y=$\frac{1}{2}$��10-x��•$\sqrt{3}$��10-x��=$\frac{\sqrt{3}}{2}$��10-x��2��
��y=$\frac{1}{2}$S��ABC=$\sqrt{3}$ʱ����$\frac{\sqrt{3}}{2}$��10-x��2=$\sqrt{3}$��
���x=��10-$\sqrt{2}$��cm����x=��10+$\sqrt{2}$��cm����ȥ����
���Ե�x=��10-$\sqrt{2}$��cmʱ���ص����ֵ�������ڡ�ABC�������һ�룮
����������֪����x=��2+$\sqrt{2}$��cm��x=��10-$\sqrt{2}$��cmʱ���ص����ֵ�������ڡ�ABC�������һ�룮
���� �����Ǽ��α任�ۺ��⣬�����漰����ת�����ʣ���ԳƵ����ʣ�ƽ�Ƶ����ʣ���ֱ�������Σ����Ǻ����Ķ��壬���ε��ж��������Ρ��ı��ε������֪ʶ���ۺ��Խ�ǿ���Ѷ����У����˶��仯�Ĺ۵��ܹ���x��ֵ������ȷ�����ǽ���ڣ�3���ʵĹؼ���


 �߽�������ϵ�д�
�߽�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��ֱ��AB��x�ύ��A��1��0������y�ύ��B��0��-2����
��ͼ��ʾ��ֱ��AB��x�ύ��A��1��0������y�ύ��B��0��-2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
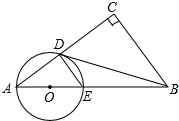 ��֪����ͼ����Rt��ABC�У���C=90�㣬��O��AB�ϣ���OΪԲ�ģ�OA��Ϊ�뾶��Բ��AC��AB�ֱ��ڵ�D��E������DE��DB������CBD=��A��
��֪����ͼ����Rt��ABC�У���C=90�㣬��O��AB�ϣ���OΪԲ�ģ�OA��Ϊ�뾶��Բ��AC��AB�ֱ��ڵ�D��E������DE��DB������CBD=��A���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ij�����ס������������˶�Ա12�������÷������ͼ��ʾ���£�
ij�����ס������������˶�Ա12�������÷������ͼ��ʾ���£�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
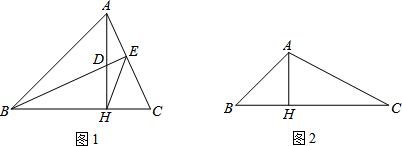
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com