
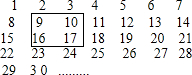 把连续的正整数1,2,3,4,…,按如图方式列成一个数表.
把连续的正整数1,2,3,4,…,按如图方式列成一个数表.分析 (1)左右相邻两个数差1,上下相邻的两个数相差为7,据此表示其它三个数,再相加即可求解;
(2)根据题意列出x+x+1+x+7+x+8=244,解一元一次方程求出x的值;
(3)令x+x+1+x+7+x+8=380,求出x的值,进而作出判断.
解答 解:(1)由图表可知:左右相邻两个数差1,上下相邻的两个数相差为7,左上角的一个数为x,
则另外三个数用含x的式子从小到大依次表示x+1;x+7;x+8,
x+x+1+x+7+x+8=4x+16.
故答案为:4x+16;
(2)根据题意可得:
x+x+1+x+7+x+8=244,
4x+16=244,
解得x=57.
答:x的值为57;
(3)假设x+x+1+x+7+x+8=380,
解得x=91.
因为91是第13行最后1个数,
所以它们不可能被(1)中的正方形框框住.
点评 本题主要考查了一元一次方程组的应用,解答本题的关键是掌握上下每列两个数相差为7,此题难度不大.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
 小明和小华在一栋大楼的前面估计楼房高度.小明说这楼有20层!小华说没有20层.为了验证他们的观点,他们在大楼两侧选择A、B两个点,经过测量AB=150米,CD=10米.∠A=30°,∠B=45°.不计两个人的身高,且A、B、C、D四个点在同一直线上.
小明和小华在一栋大楼的前面估计楼房高度.小明说这楼有20层!小华说没有20层.为了验证他们的观点,他们在大楼两侧选择A、B两个点,经过测量AB=150米,CD=10米.∠A=30°,∠B=45°.不计两个人的身高,且A、B、C、D四个点在同一直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).
已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
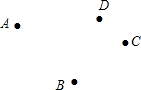 已知平面上A、B、C、D四个点,请用直尺按下列步骤要求完成画图.
已知平面上A、B、C、D四个点,请用直尺按下列步骤要求完成画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
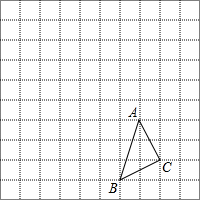 △ABC在方格中的位置如图所示.
△ABC在方格中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
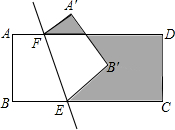 如图,矩形ABCD中,AB=2cm,BC=5cm,将四边形ABEF沿直线EF折叠,点A落在A′处,点B落在B′处,则阴影部分的周长为14cm.
如图,矩形ABCD中,AB=2cm,BC=5cm,将四边形ABEF沿直线EF折叠,点A落在A′处,点B落在B′处,则阴影部分的周长为14cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com