
【题目】如图,已知正方形![]() 与
与![]() ,点E在
,点E在![]() 上,且为
上,且为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 的反向廷长线上.请利用无刻度的直尺按下列要求画图(保留画图的痕迹).
的反向廷长线上.请利用无刻度的直尺按下列要求画图(保留画图的痕迹).
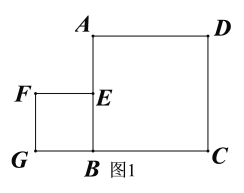
(1)在图1中,画出![]() 的中点
的中点![]() ;
;
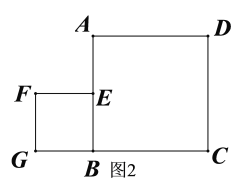
(2)在图2中,画出![]() 的垂直平分线.
的垂直平分线.
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
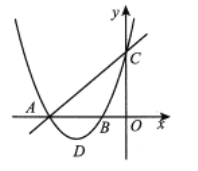
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,经过
,经过![]() ,
,![]() 两点的抛物线
两点的抛物线![]() 与
与![]() 轴的负半轴的另一交点为
轴的负半轴的另一交点为![]() ,且
,且![]()
(1)求该抛物线的解析式及抛物线顶点![]() 的坐标;
的坐标;
(2)点![]() 是射线
是射线![]() 上一点,问是否存在以点
上一点,问是否存在以点![]() ,
,![]() ,
,![]() 为顶点的三角形,与
为顶点的三角形,与![]() 相似,若存在,请求出点
相似,若存在,请求出点![]() 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
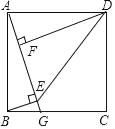
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为落实教育局“教育信息化2.0行动计划”,搭建数字化校园平台,需要购买一批电子白板和平板电脑,若购买2台电子白板和6台平板电脑共需9万元;购买3台电子白板和4台平板电脑共需11万元.
(1)求电子白板和平板电脑的单价各是多少万元?
(2)结合学校实际,该校准备购买电子白板和平板电脑共100台,其中电子白板至少购买6台且不超过24台,某商家给出了两种优惠方案,方案一:电子白板和平板电脑均打九折;方案二:买1台电子白板,送1台平板电脑.若购买电子白板a(台)所需的费用为W(万元),请根据两种优惠方案分别写出W关于a的函数关系式,并分析该校应选用哪种优惠方案购买更省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们将抛物线![]() 通过平移后得到
通过平移后得到![]() ,且设平移后所得抛物线的顶点依次为
,且设平移后所得抛物线的顶点依次为![]() ,这些顶点均在格点上,我们将这些抛物线称为“缤纷抛物线”(k为整数).
,这些顶点均在格点上,我们将这些抛物线称为“缤纷抛物线”(k为整数).
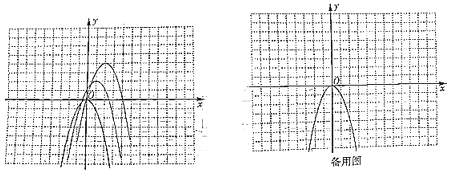
(1)![]() 的坐标为____________,直接写出平移后抛物线
的坐标为____________,直接写出平移后抛物线![]() 的解析式为____________(用k表示);
的解析式为____________(用k表示);
(2)若平移后的抛物线![]() 与抛物线
与抛物线![]() 交于点A,对称轴与抛物线
交于点A,对称轴与抛物线![]() 交于点B,若
交于点B,若![]() ,求整数k的值.
,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有三点(1,3),(3,2),(﹣2,﹣![]() ),其中两点同时在反比例函数y=
),其中两点同时在反比例函数y=![]() 的图象上,将两点分别记为A,B,另一点记为C.
的图象上,将两点分别记为A,B,另一点记为C.

(1)求反比例函数的解析式;
(2)求直线AB对应的一次函数的解析式;
(3)连接AC、BC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行
销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)于销售单价x(元
/个)之间的对应关系如图所示.
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查销售规律,求利润w(元)与销售单价x(元/个)之间的
函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试求此时这种许愿瓶的销售单价,并求出
最大利润.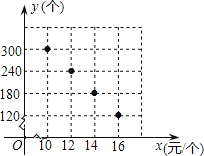
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣![]() 经过点A(1,0)和点B(5,0),与y轴交于点C.
经过点A(1,0)和点B(5,0),与y轴交于点C.
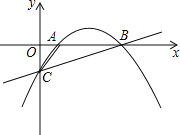
(1)求此抛物线的解析式;
(2)以点A为圆心,作与直线BC相切的⊙A,求⊙A的半径;
(3)在直线BC上方的抛物线上任取一点P,连接PB,PC,请问:△PBC的面积是否存在最大值?若存在,求出这个最大值的此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com