
【题目】正方形![]() 的边长为
的边长为![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的动点,连接
上的动点,连接![]() 并延长,交边
并延长,交边![]() 于
于![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,交边
,交边![]() 于点
于点![]() .
.
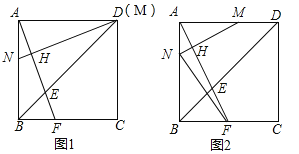
(1)如图1,若点![]() 与点
与点![]() 重合,求证:
重合,求证:![]() ;
;
(2)如图2,若点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,运动时间为
运动,运动时间为![]() .
.
①设![]() ,求
,求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
②当![]() 时,连接
时,连接![]() ,求
,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
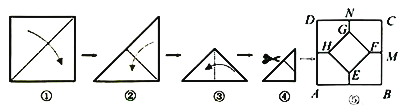
【题目】将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中![]() 是折痕.若正方形
是折痕.若正方形![]() 与五边形
与五边形![]() 的面积相等,则
的面积相等,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
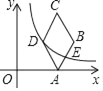
【题目】如图,菱形ABCD的顶点A在x轴的正半轴上,∠C=60°,顶点B,D的纵坐标相同,已知点B的横坐标为7![]() ,若过点D的双曲线y=
,若过点D的双曲线y=![]() (k>0)恰好过边AB的中点E,则k=_____.
(k>0)恰好过边AB的中点E,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
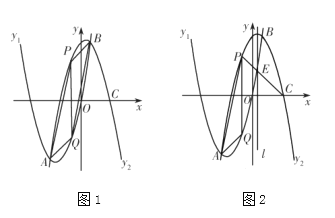
【题目】如图1,已知抛物线![]() 与抛物线
与抛物线![]() 的形状相同,开口方向相反,且相交于点
的形状相同,开口方向相反,且相交于点![]() 和点
和点![]() .抛物线
.抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() 为抛物线
为抛物线![]() 上
上![]() 两点间一动点,过点
两点间一动点,过点![]() 作直线
作直线![]() 轴,与
轴,与![]() 交于点
交于点![]() .
.
(1)求抛物线![]() 与抛物线
与抛物线![]() 的解析式;
的解析式;
(2)四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值,并写出此时点
的最大值,并写出此时点![]() 的坐标;
的坐标;
(3)如图2,![]() 的对称轴为直线
的对称轴为直线![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,在(2)的条件下,直线
,在(2)的条件下,直线![]() 上是否存在一点
上是否存在一点![]() ,使得以
,使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?如果存在,求出点
相似?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了解我市气温变化情况,记录了今年月份连续![]() 天的最低气温(单位:℃):
天的最低气温(单位:℃):![]() .关于这组数据,下列结论不正确的是( )
.关于这组数据,下列结论不正确的是( )
A.平均数是![]() B.中位数是
B.中位数是![]() C.众数是
C.众数是![]() D.方差是
D.方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
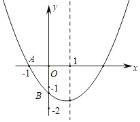
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和C(0,﹣1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc>0;②4a+2b+c>0;③4ac﹣b2<8a;④![]() ;⑤b<c.其中含所有正确结论的选项是_____.
;⑤b<c.其中含所有正确结论的选项是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点B(3,0),C(0,-2),直线L:
经过点B(3,0),C(0,-2),直线L:![]() 交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A重合).
交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A重合).
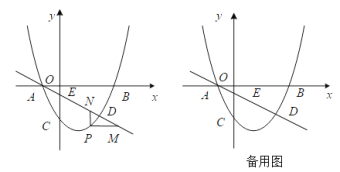
(1)求抛物线的解析式.
(2)当点P在直线L下方时,过点P作PM∥x轴交L于点M,PN∥y轴交L于点N,求PM+PN的最大值.
(3)设F为直线L上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A.
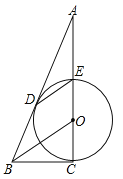
(1)求证:直线BC是⊙O的切线;
(2)若AE=2,tan∠DEO=![]() ,求AO的长.
,求AO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
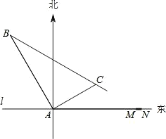
【题目】在某飞机场东西方向的地面 l 上有一长为 1km 的飞机跑道 MN(如图),在跑道 MN的正西端 14.5 千米处有一观察站 A.某时刻测得一架匀速直线降落的飞机位于点 A 的北偏西30°,且与点 A 相距 15 千米的 B 处;经过 1 分钟,又测得该飞机位于点 A 的北偏东 60°,且与点 A 相距 5![]() 千米的 C 处.
千米的 C 处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道 MN 之间?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com