
【题目】四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为![]() 的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=
的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=![]() EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】我们知道:三角形的三条角平分线交于一点,这个点称为三角形的内心(三角形内切圆的圆心).现在规定:如果四边形的四个角的角平分线交于一点,我们把这个点也成为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)如图1,已知点O是四边形ABCD的内心,求证:AB+CD=AD+BC.
(3)如图2,Rt△ABC中,∠C=90°.O是△ABC的内心.若直线DE截边AC,BC于点D,E,且O仍然是四边形ABED的内心.这样的直线DE可画多少条?请在图2中画出一条符合条件的直线DE,并简单说明作法.
(4)问题(3)中,若AC=3,BC=4,满足条件的一条直线DE∥AB,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明拿两个大小不等直角三角板作拼图,如图①小三角板的斜边与大三角板直角边正好重合,已知:AD=1,∠B=∠ACD=30°.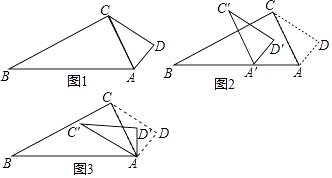
(1)AB的长;四边形ABCD的面积=(直接填空);
(2)如图2,若小明将小三角板ACD沿着射线AB方向平移,设平移的距离为m(平移距离指点A沿AB方向锁经过的线段长度),当点D平移到线段大三角板ABC的边上时,求出相应的m的值;
(3)如图3,小明将小三角板ACD绕点A顺时针旋转一个角α(0°<α<180°),记旋转中的△ACD为△AC′D′,在旋转过程中,设C′D′所在的直线与直线BC交于点P,与直线AB交于点Q,是否存在这样的P、Q两点,使△BPQ为等腰三角形?若存在,请直接求出此时D′Q的长;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 ;
(2)线段CD由线段AB经过怎样平移得到?
(3)求F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)老张种植柑橘的成本是800元/吨,当客商采购量是多少时,老张在这次销售柑橘时获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
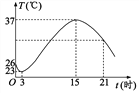
【题目】温度的变化是人们经常谈论的话题,请根据图象与同伴讨论某天温度变化的情况.
(1)这一天的最高温度是多少?是在几时到达的?最低温度呢?
(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?
(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线 AC、BD 相交成的锐角α=30°,若 AC=8,BD=6,则□ABCD的面积是( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个零件如图所示

(1)请说明∠BDC >∠A
(2)按规定∠A等于90°,∠B和∠C应分别等于32°和21°,检验工人量得∠BDC等于148°,就断定这个零件不合格,这是为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com