
分析 (1)直接把点B的横坐标等于2代入直线y=-2x+5求出y的值,进而可得出反比例函数的解析式;
(2)根据A、B两点在y=$\frac{k}{x}$(k≠0,x>0)上,可得出m(-2m+5)=n(-2n+5),由此可得出m与n之间的函数关系式;
(3)作AN⊥DO,BP⊥CO,根据D,C的坐标可得出,DO,CO的长,由M为DO中点可知MO=$\frac{5}{2}$=CO.故AN=m.由(2)得m=-n+$\frac{5}{2}$,AN=-n+$\frac{5}{2}$.再由B(n,-2n+5)可知OP=n,故可得出PC=AN,根据ASA定理得出△DNA≌△BPC,故AD=BC,求出△BOC面积的表达式,作EQ⊥x轴,同理可得△BPC≌△CQE,再求出BP,QE,OQ的长即可得出结论.
解答 解:(1)∵点B在y=-2x+5上,
∴B(2,1),
∴y=$\frac{2}{x}$;
(2)∵A(m,-2m+5),B(n,-2n+5),A、B两点在y=$\frac{k}{x}$(k≠0,x>0)上,
∴m(-2m+5)=n(-2n+5),
∴-2m2+5m=-2n2+5n,即2(n2-m2)=5(n-m),即2(n-m)(n+m)=5(n-m).
又∵n-m≠0,
∴n+m=$\frac{5}{2}$,
∴m=-n+$\frac{5}{2}$;
(3)作AN⊥DO,BP⊥CO,
∵D(0,5),C($\frac{5}{2}$,0),
∴DO=5,C0=$\frac{5}{2}$,
∵M为DO中点,
∴MO=$\frac{5}{2}$=CO.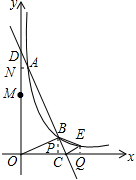
又∵A(m,-2m+5),
∴AN=m.
∵由(2)得m=-n+$\frac{5}{2}$,
∴AN=-n+$\frac{5}{2}$.
∵B(n,-2n+5)
∴OP=n,
∴PC=CO-PO=-n+$\frac{5}{2}$=AN,
在△DNA与△BPC中,
$\left\{\begin{array}{l}∠AND=∠CPB=90°\\ PC=AN\\∠DAN=∠BCP\end{array}\right.$,
∴△DNA≌△BPC(ASA),
∴AD=BC,
∴△BOC是以MO、BO、AD的长为三边构成的三角形,
∴S△BOC=$\frac{25}{16}$=$\frac{1}{2}$OC•BP=$\frac{1}{2}$×$\frac{5}{2}$BP
∴BP=$\frac{5}{4}$,
∴-2n+5=$\frac{5}{4}$n=$\frac{15}{8}$,
∴B($\frac{15}{8}$,$\frac{5}{4}$)
∴k=$\frac{75}{32}$,
∴y=$\frac{75}{32x}$,
∴OP=$\frac{15}{8}$,
∴PC=$\frac{5}{2}$-$\frac{15}{8}$=$\frac{5}{8}$,
∵等腰直角△BCE,∠BCE=90°,BC=CE,
∴作EQ⊥x轴,
∴△BPC≌△CQE,
∴BP=CQ=$\frac{5}{4}$,QE=PC=$\frac{5}{8}$
∴OQ=$\frac{5}{2}$+$\frac{5}{4}$=$\frac{15}{4}$,
∴E($\frac{15}{4}$,$\frac{5}{8}$) 当x=$\frac{15}{4}$时,y=$\frac{5}{8}$,
∴点E在此双曲线上.
点评 本题考查的是反比例函数综合题,涉及到反比例函数与一次函数图象上点的坐标问题,全等三角形的判定与性质等知识,难度适中.


科目:初中数学 来源: 题型:选择题
| A. | -6与-7之间 | B. | -7与-8之间 | C. | 7与8之间 | D. | 6与7之间 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 次数m | 余额n(元) |
| 1 | 50-0.5 |
| 2 | 50-1.0 |
| 3 | 50-1.5 |
| 4 | 50-2.0 |
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
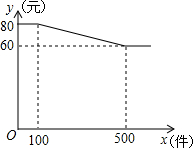 某服装厂A装,其单价y(元)与批发数量x(件)(x为正整数)之间的函
某服装厂A装,其单价y(元)与批发数量x(件)(x为正整数)之间的函查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com