
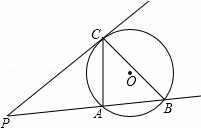
已知:如图,P是⊙O外一点,过点P引圆的切线PC(C为切点)和割线PAB,分别交⊙O于A、B,连接AC,BC.
(1)求证:∠PCA=∠PBC;
(2)利用(1)的结论,已知PA=3,PB=5,求PC的长.
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
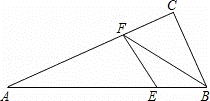
如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连接FB,则tan∠CFB的值等于( )
A. 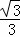 B.
B. C.
C. D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A. 1,2,3 B.1,1, C.1,1,
C.1,1,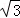 D. 1,2,
D. 1,2,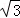
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )

A. 4km B.2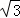 km C.2
km C.2 km D. (
km D. (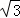 +1)km
+1)km
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标;
(2)求出在整个平移过程中,△ABC扫过的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com