
| 产品 | A | B |
| 进价 | 3000元/千克 | 4000元/千克 |
| 售价 | 4150元/千克 | 5500元/千克 |
分析 (1)设该经销商购进A产品x千克,购进B产品y千克,根据两种产品的总重量结合总价=单价×购进数量,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)根据销售收入-成本=利润,列式计算即可得出结论;
(3)分别求出销售每千克A、B产品的利润以及厂家回收每千克A、B产品的亏损,设本次该经销商购进A产品m千克、B产品n千克时可在销售中获利89890元,根据两种产品共购进100千克结合盈利-亏损=利润,即可得出关于m、n的二元一次方程组,解之即可得出结论.
解答 解:(1)设该经销商购进A产品x千克,购进B产品y千克,
根据题意得:$\left\{\begin{array}{l}{x+y=50}\\{3000x+4000y=170000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=30}\\{y=20}\end{array}\right.$.
答:该经销商购进A产品30千克,购进B产品20千克.
(2)4150×30×(1-10%)+5500×20×(1-20%)+3000×60%×30×10%+4000×60%×20×20%-170000=45050(元).
答:他在这次销售中获利45050元.
(3)销售每千克A产品利润4150-3000=1150(元),
销售每千克B产品利润5500-4000=1500(元),
厂家回收每千克A产品亏损3000×(1-60%)=1200(元),
厂家回收每千克B产品亏损4000×(1-60%)=1600(元).
设本次该经销商购进A产品m千克、B产品n千克时可在销售中获利89890元,
根据题意得:$\left\{\begin{array}{l}{m+n=100}\\{1150×0.9m-1200×0.1m+1500×0.8n-1600×0.2n=89890}\end{array}\right.$,
整理得:$\left\{\begin{array}{l}{m+n=100}\\{183m+176n=17978}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=54}\\{n=46}\end{array}\right.$.
答:本次该经销商购进A产品54千克、B产品46千克时可在销售中获利89890元.
点评 本题考查了二元一次方程组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据数量关系列式计算;(3)找准等量关系,正确列出二元一次方程组.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:填空题
 如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是40cm.
如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是40cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:已知线段a、b
如图:已知线段a、b查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 7 | 4 | 0 |
| 乙 | 7 | 7.5 | 5.4 | 1 |
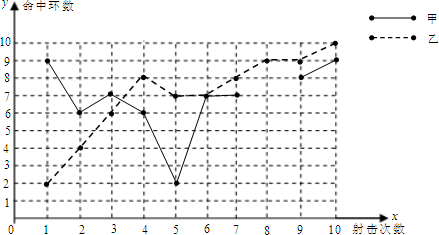
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com