练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】学校到- -家文具店给九年级学生购买考试用文具包,该文具店规一次购买个以上，可享受八折优惠.若给九年级学生每人购买一个，则不能享受八折优惠，需付款元;若再多买个就可享受八折优惠，并且同样只需付款元.求该校九年级学生的总人数. (列分式方程解答)

    【答案】该校九年级学生的总人数是人.

    【解析】

    首先设九年级学生有x人，根据“给九年级学生每人购买一个，不能享受8折优惠，需付款2520元”可得每个文具包的花费是元，根据“若多买70个，就可享受8折优惠，同样只需付款2520元”可得每个文具包的花费是元，根据题意可得方程即可

    解:设该校九年级学生的总人数是人，

    由题意得，

    解得: ，

    经检验: 是原分式方程的解，且符合题意．

    答:该校九年级学生的总人数是人．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形中，，，∠，点是的中点，点在的边上，若为等腰三角形，则的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明家的洗手盆上装有一种抬启式水龙头（如图1），完全开启后，水流路线呈抛物线，把手端点A，出水口B和落水点C恰好在同一直线上，点A至出水管BD的距离为12cm，洗手盆及水龙头的相关数据如图2所示，现用高10.2cm的圆柱型水杯去接水，若水流所在抛物线经过点D和杯子上底面中心E，则点E到洗手盆内侧的距离EH为_________cm．

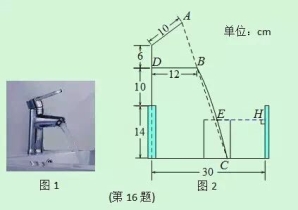
    （第16题图）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=kx+b（k≠0）与抛物线y=ax2（a≠0）交于A，B两点，且点A的横坐标是-2，点B的横坐标是3，则以下结论：

    ①抛物线y=ax2（a≠0）的图象的顶点一定是原点；

    ②x＞0时，直线y=kx+b（k≠0）与抛物线y=ax2（a≠0）的函数值都随着x的增大而增大；

    ③AB的长度可以等于5；

    ④△OAB有可能成为等边三角形；

    ⑤当-3＜x＜2时，ax2+kx＜b，

    其中正确的结论是（ ）

    A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（探究发现）

    如图1，在△ABC中，点P是内角∠ABC和外角∠ACD的角平分线的交点，试猜想∠P与∠A之间的数量关系，并证明你的猜想．

    （迁移拓展）

    如图2，在△ABC中，点P是内角∠ABC和外角∠ACD的n等分线的交点，即∠PBC＝∠ABC，∠PCD＝∠ACD，

    试猜想∠P与∠A之间的数量关系，并证明你的猜想．

    （应用创新）

    已知，如图3，AD、BE相交于点C，∠ABC、∠CDE、∠ACE的角平分线交于点P，∠A＝35°，∠E＝25°，则∠BPD＝　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，，已知中，，，的顶点、分别在边、上，当点在边上运动时，随之在上运动，的形状始终保持不变，在运动的过程中，点到点的最小距离为（ ）

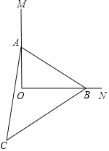
    A. 5 B. 7 C. 12 D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

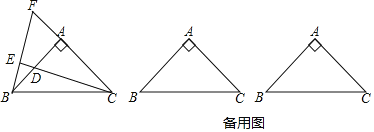
    【题目】如图，△ABC中，AB=AC，∠BAC=90°，点D是直线AB上的一动点（不和A、B重合），BE⊥CD于E，交直线AC于F．

    (1)点D在边AB上时，证明：AB=FA+BD；

    (2)点D在AB的延长线或反向延长线上时，(1)中的结论是否成立？若不成立，请画出图形并直接写出正确结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

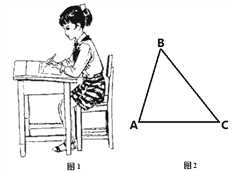
    【题目】人写字时眼睛和笔端的距离超过30cm时则符合保护视力的要求.图1是一位同学的坐姿，把她的眼睛B、肘关节C和笔端A的位置关系抽象成图2的△ABC，BC=30cm,AC=22cm,∠ACB=530,她的这种坐姿符合保护视力的要求吗？请说明理由.（参考数据：sin530≈0.8,cos530≈0.6,tan530≈1.3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC，直线PQ垂直平分AC，与边AB交于E，连接CE，过点C作CF平行于BA交PQ于点F，连接AF．

    （1）求证：△AED≌△CFD；

    （2）求证：四边形AECF是菱形．

    （3）若AD=3，AE=5，则菱形AECF的面积是多少？

    查看答案和解析>>

    同步练习册答案