
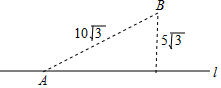
 如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5$\sqrt{3}$千米的地方有一居民点B,A、B的直线距离是10$\sqrt{3}$千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{3}{8}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5$\sqrt{3}$千米的地方有一居民点B,A、B的直线距离是10$\sqrt{3}$千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{3}{8}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.) 分析 要求所用行车时间最短,就要计算好行驶的路线,可以设在公路上行驶x千米,根据题意,找出可以运用勾股定理的直角三角形,运用勾股定理求解.
解答 解:如图所示,公路上行驶的路线是AD,草地上行驶的路线是DB,设AD的路程为x千米,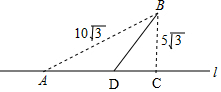
由已知条件AB=10$\sqrt{3}$千米,BC=5$\sqrt{3}$千米,BC⊥AC,知
AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=15千米.
则CD=AC-AD=(15-x)千米,
BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=$\sqrt{(5\sqrt{3})^{2}+(15-x)^{2}}$km,
设走的行驶时间为y,则
y=$\frac{x}{80}$+$\frac{\sqrt{75+(15-x)^{2}}}{40}$.
整理为关于x的一元二次方程得
3x2+(160y-120)x-6400y2+1200=0.
因为x必定存在,所以△≥0.即
(160y-120)2-4×3×(1200-6400y2)≥0.
化简得102400y2-38400y≥0.
解得y≥$\frac{3}{8}$,
即消防车在出发后最快经过$\frac{3}{8}$小时可到达居民点B.
故答案为:$\frac{3}{8}$.
点评 本题考查的是在直角三角形中勾股定理的运用,画出图形构建直角三角形是关键,根据一元二次不等式的求解,可以计算出解的最小值,以便求出最短路程.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
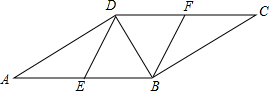 如图,在?ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
如图,在?ABCD中,E,F分别为边AB,CD的中点,BD是对角线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 处理污水量(吨/月) | 240 | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
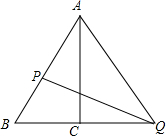 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=6.动点P从点A出发沿AB方向以每秒2个单位的速度运动,同时动点Q从点C出发沿射线BC以每秒2个单位的速度运动,当点P到达点B时,P,Q同时停止运动,连结PQ,QA.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=6.动点P从点A出发沿AB方向以每秒2个单位的速度运动,同时动点Q从点C出发沿射线BC以每秒2个单位的速度运动,当点P到达点B时,P,Q同时停止运动,连结PQ,QA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{3}{2}$或2 | C. | $\frac{3}{2}$或6 | D. | 2、$\frac{3}{2}$或6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com