
【题目】如图,![]() ,OA=OB=6,点C,D分别为线段OA,OB上的动点(C,D不与A,B重合),则AD+CD+BC的最小值为( )
,OA=OB=6,点C,D分别为线段OA,OB上的动点(C,D不与A,B重合),则AD+CD+BC的最小值为( )

A.4B.6C.![]() D.
D.![]()
【答案】B
【解析】
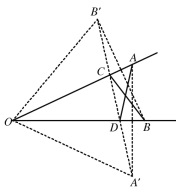
作A关于ON的对称点A',作B关于OM的对称点B',连接A'B'交ON、OM于C、D,,此时AD+CD+BC最小,再连接O B',O A',可得△O A' B'为等边三角形,则最小值为6.
如图所示,作A关于ON的对称点A',作B关于OM的对称点B',连接A'B'交ON、OM于C、D,,此时AD+CD+BC最小值为A' B',连接O B',O A',
由轴对称可知,O B'=OB=6,O A'=OA=6,∠B'OC=∠COD=∠A'OD=20°,
∠B'O A'=60°,而O B'= O A',∴△O A' B'为等边三角形,∴A' B'=6,即AD+CD+BC的最小值为6,故选B.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.

(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
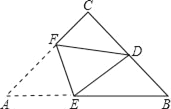
【题目】如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB、BC延长线于F、E,以下四个结论:(1)∠EAD=∠EDA,(2)DF∥AC;(3)∠FDE=90°;(4)∠B=∠CAE,恒成立的结论有( )个.

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=3,∠B=30°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=30°,DE交线段AC于点E.

(1)D点运动到图1位置时,∠BDA=75°,则∠EDC=______,∠DEC=________;
(2)D点运动到图2位置时,当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在变化,判断当△ADE是等腰三角形时,∠BDA等于多少度(请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象。
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
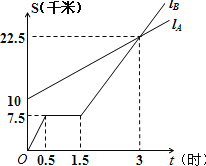
(1)B出发时与A相距 千米.
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com