
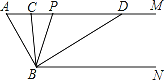
【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
【答案】(1)∠CBD=50°;(2)不变,∠APB:∠ADB=2:1;(3)∠ABC=25°.
【解析】
(1)由平行线的性质可求得∠ABN,再根据角平分线的定义和整体思想可求得∠CBD;
(2)由平行线的性质可得∠APB=∠PBN,∠ADB=∠DBN,再由角平分线的定义可求得结论;
(3)由平行线的性质可得到∠ACB=∠CBN=60°+∠DBN,结合条件可得到∠DBN=∠ABC,且∠ABC+∠DBN=60°,可求得∠ABC的度数.
(1)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°﹣80°=100°,
∴∠ABP+∠PBN=100°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=100°,
∴∠CBD=∠CBP+∠DBP=50°;
(2)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=100°,∠CBD=50°,
∴∠ABC+∠DBN=50°,
∴∠ABC=25°.


科目:初中数学 来源: 题型:
【题目】对下列代数式作出解释,其中不正确的是( )
A. a-b:今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a-b)岁
B. a-b:今年小明b岁,小明的爸爸a岁,则小明出生时,他爸爸为(a-b)岁
C. ab:长方形的长为acm,宽为bcm,长方形的面积为ab ![]()
D. ab:三角形的一边长为acm,这边上的高为bcm,此三角形的面积为ab ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.5元,花35元购买粽子的个数与花20元购买咸鸭蛋的个数相同.粽子与咸鸭蛋的价格各是多少?
【答案】粽子和咸鸭蛋的单价分别为每个3.5元、2元
【解析】试题分析:设咸鸭蛋的价格为x元,则粽子的价格为(1.5+x)元,根据花35元购买粽子的个数与花20元购买咸鸭蛋的个数相同,列出分式方程,求出方程的解得到x的值,即可得到结果.
试题解析:
解:设咸鸭蛋的价格为x元,则粽子的价格为(1.5+x)元,
根据题意得:
![]() ,
,
去分母得:35x=30+20x,
解得:x=2,
经检验x=2是分式方程的解,且符合题意,
1.5+x=1.5+2=3.5(元),
故咸鸭蛋的价格为2元,粽子的价格为3.5元.
点睛:此题考查了分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.
【题型】解答题
【结束】
24
【题目】某书店为了迎接“读书节”制定了活动计划,陈经理查看计划书发现:A类图书的标价是B类图书标价的1.5倍,若顾客用1080元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少20本.请求出A、B两类图书的标价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于不等式组 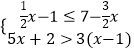 下列说法正确的是( )
下列说法正确的是( )
A.此不等式组无解
B.此不等式组有7个整数解
C.此不等式组的负整数解是﹣3,﹣2,﹣1
D.此不等式组的解集是﹣ ![]() <x≤2
<x≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
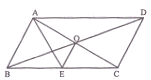
【题目】如图□ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=600,AB=![]() BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=![]() BC 成立的个数有( )
BC 成立的个数有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.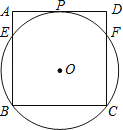
(1)求证:PF平分∠BFD.
(2)若tan∠FBC= ![]() ,DF=
,DF= ![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=3,AB=4,求菱形ADCF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1和∠2互补,∠C=∠EDF.
(1)判断DF与EC的关系为 .
(2)试判断DE与BC的关系,并说明理由.
(3)试判断∠DEC与∠DFC的关系并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com