
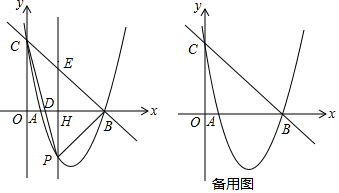
���� ��1����B��C���������������߽���ʽ��
��2�������ֱ��BC�Ľ���ʽ�������t��ʾ��PE�ij�����һ���ɱ�ʾ����PBC������������ö��κ��������ʿ���������ֵ��
��3������t��ʾ��P��H��E �����꣬�ɣ�2����֪��BHEΪ����ֱ�������Σ������BE=$\sqrt{2}$��-t+5������PE=PB��BE=BP��BE=PE����������ֱ�õ�����t�ķ��̣������t��ֵ��������P������꣮
��� �⣺
��1����B��5��0����C��0��5����
��c=5��0=25a-30+c�����a=1��
�������߽���ʽΪy=x2-6x+5��
��2����B��5��0����C��0��5����
��ֱ��BC����ʽΪy=-x+5��
��P�ĺ�����Ϊt������PB��PC��PC��x�ύ�ڵ�D������P��y���ƽ���߽�x���ڵ�H����ֱ��BC�ڵ�E��
��P��t��t2-6t+5����E��t��-t+5����
��PE=-t+5-��t2-6t+5��=-t2+5t��
��S��PBC=$\frac{1}{2}$OB•PE=$\frac{1}{2}$��5��-t2+5t��=-$\frac{5}{2}$��t-$\frac{5}{2}$��2+$\frac{125}{8}$��
��-$\frac{5}{2}$��0��
��S��PBC�����ֵ�����ֵΪ$\frac{125}{8}$��
�ʴ�Ϊ�����
��3�����ڣ��������£�
�������֪P��t��t2-6t+5������H��t��0����E��t��-t+5�����ҡ�BHEΪ����ֱ�������Σ�
��BE=$\sqrt{2}$BH=$\sqrt{2}$��5-t����
�ߡ�BPEΪ���������Σ�
����PE=PB��BE=BP��BE=PE���������
�ٵ�PE=PBʱ�����ڡ�PEB=45�㣬
���PEBΪ����ֱ�������Σ���P��A�㴦����P��1��0�����������⣻
�ڵ�BE=BPʱ������PE��BH��
��HE=HP������E���P����x��Գƣ�
��-t+5+t2-6t+5=0�����t=2��t=5���������⣬��ȥ����
��P��2��-3����
�۵�BE=PEʱ��
�ߡ�EHBΪ����ֱ�������Σ�
��BE=$\sqrt{2}$HB=$\sqrt{2}$��5-t������PE=|-t2+5t|��
��|-t2+5t|=$\sqrt{2}$��5-t�������t=��$\sqrt{2}$��t=5���������⣬��ȥ����
��P��$\sqrt{2}$��7-6$\sqrt{2}$����-$\sqrt{2}$��7+6$\sqrt{2}$����
���Ͽ�֪�������������ĵ�P��������Ϊ��1��0����2��-3����$\sqrt{2}$��7-6$\sqrt{2}$����-$\sqrt{2}$��7+6$\sqrt{2}$����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ�����������ε���������κ��������ʡ����������ε����ʡ�����˼�뼰��������˼���֪ʶ���ڣ�1����ע�����ϵ������Ӧ�ã��ڣ�2������t��ʾ����PBC������ǽ���Ĺؼ����ڣ�3������t�ֱ��ʾ��BE��PE��BP�ij��ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
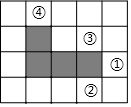 �ڷ���ֽ�У�ѡ�������Ţ٢ڢۢ��е�һ��С������Ϳ�ڣ���ͼ����Ӱ���ֹ������ĶԳ�ͼ�Σ���С�����ε�����ǣ�������
�ڷ���ֽ�У�ѡ�������Ţ٢ڢۢ��е�һ��С������Ϳ�ڣ���ͼ����Ӱ���ֹ������ĶԳ�ͼ�Σ���С�����ε�����ǣ�������| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2017 | B�� | 2017 | C�� | $-\frac{1}{2017}$ | D�� | $\frac{1}{2017}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 45�� | C�� | 50�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
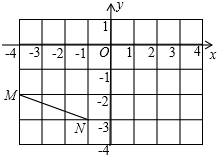 �߶�MN��ֱ������ϵ�е�λ����ͼ��ʾ����MN�Ƶ�M��ʱ����ת90��õ��߶�M1N1�����N�Ķ�Ӧ��N1������Ϊ��������
�߶�MN��ֱ������ϵ�е�λ����ͼ��ʾ����MN�Ƶ�M��ʱ����ת90��õ��߶�M1N1�����N�Ķ�Ӧ��N1������Ϊ��������| A�� | ��0��0�� | B�� | ��-5��-4�� | C�� | ��-3��1�� | D�� | ��-1��-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 121 | B�� | ��$\sqrt{11}$ | C�� | $\sqrt{11}$ | D�� | -$\sqrt{11}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com