
分析 (1)根据分式除法的法则,将除法转化为乘法;将分子、分母分解因式,约分相乘即可;
(2)根据分式除法的法则,将除法转化为乘法;将分子、分母分解因式,约分相乘即可.
解答 解:(1)原式=$\frac{a(a-2b)}{b(b-a)}÷(\frac{{a}^{2}}{a-b}×\frac{2b-a}{2ab})=\frac{a(a-2b)}{b(b-a)}÷\frac{a(2b-a)}{2b(a-b)}$=$\frac{a(a-2b)}{b(b-a)}×\frac{2b(a-b)}{a(2b-a)}=2$;
(2)原式=$\frac{(a+b)^{2}(a-b)^{2}}{{b}^{2}}×\frac{1}{{a}^{3}(a+b)^{3}}×\frac{{a}^{2}{b}^{2}}{(a-b)^{2}}=\frac{1}{{a}^{2}-ab}$.
点评 本题主要考查分式的乘除法.熟记分式的除法法则且能够熟练将多项式因式分解是解决此题的关键.


科目:初中数学 来源: 题型:解答题
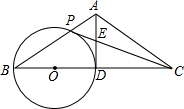 已知:如图,在等腰△ABC中,AB=AC,点D是边BC的中点,以BD为直径作⊙O,交边AB于点P,连接PC交AD于点E,且AE=DE.
已知:如图,在等腰△ABC中,AB=AC,点D是边BC的中点,以BD为直径作⊙O,交边AB于点P,连接PC交AD于点E,且AE=DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com