
 如图,在平面直角坐标系中,已知点A(2,0),B(0,3),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )
如图,在平面直角坐标系中,已知点A(2,0),B(0,3),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )| A. | (-3,2) | B. | (-3,1) | C. | (2,1) | D. | (-2,1) |
分析 作CD⊥y轴于点D,如图,根据旋转的性质得∠ABC=90°,BC=BA,再利用等角的余角相等得到∠CBD=∠A,则可证明△ABO≌△BCD得到BD=OA=2,CD=OB=3,然后根据第二象限内点的坐标特征写出C点坐标.
解答 解:作CD⊥y轴于点D,如图,
∵A(2,0),B(0,3),
∴OA=2,OB=3,
∵线段AB绕点B顺时针旋转90°至CB,
∴∠ABC=90°,BC=BA,
∵∠ABO+∠A=90°,∠ABO+∠CBD=90°,
∴∠CBD=∠A,
在△ABO和△BCD中
$\left\{\begin{array}{l}{∠AOB=∠BDC}\\{∠A=∠C}\\{AB=BC}\end{array}\right.$,
∴△ABO≌△BCD,
∴BD=OA=2,CD=OB=3,
∴OD=OB-BD=3-2=1,
∴C点坐标为(-3,1).
故选B.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.解决本题的关键是作CD⊥y轴于点D后求出CD和OD的长.


科目:初中数学 来源: 题型:填空题
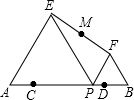 如图,C、D是线段AB上两点,且AC=BD=$\frac{1}{6}$AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点.在点P从点C移动到点D时,点M运动的路径长度为2.
如图,C、D是线段AB上两点,且AC=BD=$\frac{1}{6}$AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点.在点P从点C移动到点D时,点M运动的路径长度为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x<1\\ x<2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x<1\\ x>2\end{array}\right.$ | C. | $\left\{\begin{array}{l}x>1\\ x>2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x>1\\ x<2\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )
将矩形ABCD绕点A逆时针旋转得到矩形AEGH,若点E恰好落在AC上,EG交AD于点F,如图,已知AB=3,AC=5,则FG的长为( )| A. | 2 | B. | $\frac{7}{4}$ | C. | $\frac{9}{4}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com