
(12分)如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE,等边△BCF。
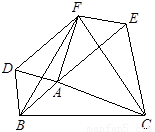
(1)求证:四边形DAEF平行四边形;
(2)(2)探究下列问题:(只填满足的条件,不需要证明)
①当∠A= 时,四边形DAEF是矩形;
②当△ABC满足 条件时,四边形DAEF是菱形;
③当△ABC满足 条件时;以D、A、E、F为顶点的四边形不存在
(1)DAEF为平行四边形。(2)∠A=150°;AB=AC时;∠A=60°时。
【解析】
试题分析:
(1)如图:三角形ABD,三角形ACE,三角形BCF都是等边三角形
∵∠DBF=60°,∠FBA=∠ABC
而DB=AB, BF=BC
△DBF≌△ABC
∴DF=AC=AE
同理可证:DA=FE
所以:DAEF为平行四边形
(2)①如果∠DAE=90°,则DAEF为矩形
则必须∠BAC=360°-2×60°-90°=150°
(另一种情况,BC为短边,F将落在DAECB的包围之中, ∠DAE=2×60°+∠BAC>90°,DAEF不可能为矩形,而BC为短边, ∠BAC<90°)
②如果:DA=AE,则:DAEF为菱形
则必须:AB=AC
③如果: ∠BAC=60°
则: ∠DAE=3×60°=180°
D,A,E共线,所以:以D、A、E、F为顶点的四边形不存在
考点:四边形判定性质综合应用
点评:此种试题,比较难,过程繁琐,需要结合学过的四边形的判定和性质以及相关的证明方法,考查学生对几何证明题的综合应用。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
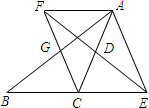 如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.
如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.查看答案和解析>>
科目:初中数学 来源: 题型:
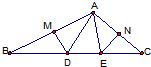 15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=
15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=查看答案和解析>>
科目:初中数学 来源: 题型:
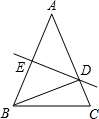 如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为
如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.
如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com