
如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点,OA、OB的长度分别为a和b,且满足 . . |
| (1)判断△AOB的形状. |
 |
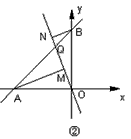
(2)如图②,正比例函数 的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长. 的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长. |
 |
| (3)如图③,E为AB上一动点,以AE为斜边作等腰直角△ADE,P为BE的中点,连结PD、PO,试问:线段PD、PO是否存在某种确定的数量关系和位置关系?写出你的结论并证明. |
 |
| (1)等腰直角三角形 ∵  ∴ ∴ ∴  ∵∠AOB=90° ∴△AOB为等腰直角三角形; (2)∵∠MOA+∠MAO=90°,∠MOA+∠MOB=90° ∴∠MAO=∠MOB ∵AM⊥OQ,BN⊥OQ ∴∠AMO=∠BNO=90° 在△MAO和△BON中  ∴△MAO≌△NOB ∴OM=BN,AM=ON,OM=BN ∴MN=ON-OM=AM-BN=5 ; (3)PO=PD且PO⊥PD 如图,延长DP到点C,使DP=PC,连结OP、OD、OC、BC 在△DEP和△CBP  ∴△DEP≌△CBP ∴CB=DE=DA,∠DEP=∠CBP=135° 在△OAD和△OBC  ∴△OAD≌△OBC ∴△OAD≌△OBC ∴OD=OC,∠AOD=∠COB ∴△DOC为等腰直角三角形 ∴PO=PD,且PO⊥PD. |
 |


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com