
分析 (1)先根据有理数乘方的法则、数的开方法则及绝对值的性质分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先去分母,把分式方程化为整式方程,求出x的值,代入最简公分母进行检验即可;
(3)先算括号里面的,再算除法,最后算减法,选取合适的x的值代入进行计算即可.
解答 解:(1)原式=-1+3-2+1-3+4
=2;
(2)方程两边同时乘以x-1得,2-(x+2)=3(x-1),解得x=$\frac{3}{4}$,
把x=$\frac{3}{4}$代入x-1得,$\frac{3}{4}$-1=-$\frac{1}{4}$≠0,
故x=$\frac{3}{4}$是原分式方程的根;
(3)原式=$\frac{2}{m+1}$-$\frac{m-2}{(m+1)(m-1)}$÷$\frac{m(m-2)}{(m-1)^{2}}$
=$\frac{2}{m+1}$-$\frac{m-2}{(m+1)(m-1)}$•$\frac{(m-1)^{2}}{m(m-2)}$
=$\frac{2}{m+1}$-$\frac{m-1}{m(m+1)}$
=$\frac{2m-m+1}{m(m+1)}$
=$\frac{1}{m}$,
当m=2时,原式=$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.


科目:初中数学 来源: 题型:解答题
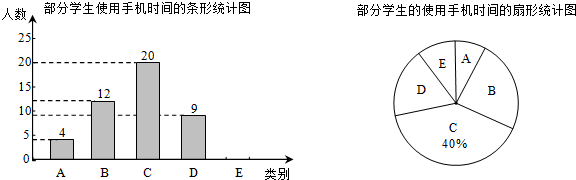
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
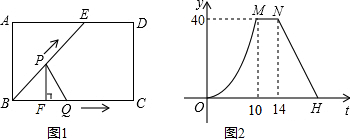
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
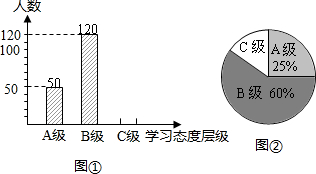 某地教育部门对九年级学生的“学习态度”进行了一次抽样调查,把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣,要求被调查的学生从A、B、C三项中必选且只能选择一项,结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
某地教育部门对九年级学生的“学习态度”进行了一次抽样调查,把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣,要求被调查的学生从A、B、C三项中必选且只能选择一项,结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
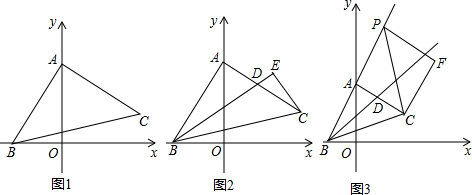
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 捐款金额(元) | 5 | 10 | 20 | 50 |
| 人数(人) | 10 | 13 | 12 | 15 |
| A. | 12.5人 | B. | 15元 | C. | 10元 | D. | 20元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
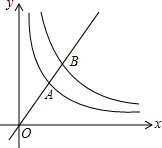 如图,在平面直角坐标系中,O为原点,直线y=kx(k>0)与双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)分别交于A,B两点,则$\frac{OB}{OA}$=$\sqrt{2}$.
如图,在平面直角坐标系中,O为原点,直线y=kx(k>0)与双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)分别交于A,B两点,则$\frac{OB}{OA}$=$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com