
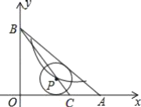
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 的圆心
的圆心![]() 在线段
在线段![]() 上,且⊙
上,且⊙![]() 与边
与边![]() ,
,![]() 都相切.若反比例函数
都相切.若反比例函数![]() (
(![]() )的图象经过圆心
)的图象经过圆心![]() ,则
,则![]() ________.
________.
【答案】![]() .
.
【解析】
设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,(见详解图)用面积法可求出⊙P的半径,然后通过等腰直角三角形的性质可求出CD,从而得到点P的坐标,即可求出k的值.
设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,如图所示.
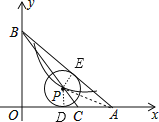
则有PD⊥OA,PE⊥AB.
设⊙P的半径为r,
∵AB=5,AC=1,
∴S△APB=![]() ABPE=
ABPE=![]() r,S△APC=
r,S△APC=![]() ACPD=
ACPD=![]() r.
r.
∵∠AOB=90°,OA=4,AB=5,
∴OB=3.
∴S△ABC=![]() ACOB=
ACOB=![]() ×1×3=
×1×3=![]() .
.
∵S△ABC=S△APB+S△APC,
∴![]() =
=![]() r+
r+![]() r.
r.
∴r=![]() .
.
∴PD=![]() .
.
又∵OB=OC=3,可知△OBC为等腰直角三角形,
∴△PDC为等腰直角三角形,
∴CD=PD=![]() .
.
∴OD=OC-CD=3-![]() =
=![]() .
.
∴点P的坐标为(![]() ,
,![]() ).
).
∵反比例函数y=![]() (k≠0)的图象经过圆心P,
(k≠0)的图象经过圆心P,
∴k=![]() ×
×![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某学校为了解高二年级男生定点投篮的情况,随机选取该校高二年级部分男生进行测试,每人投篮五次,以下是根据每人投中次數绘制的统计图的一部分,
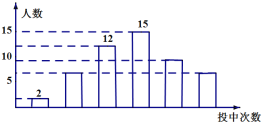
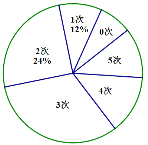
根据以上信息解答下列问题:
(1)被调查的男生中,投中次数为2次的有_____人,投中次数为1次的男生人数占被调查男生总数的百分比为_____%;
(2)被调查男生的总数为_____人,扇形统计图中投中次数为3次的圆心角的度数为_____;
(3)若该校高二年级男生有200人,根据调查结果,估计该年级男生投中次数不少于3次的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
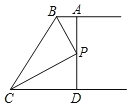
【题目】如图,两条射线BA//CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,分别交AB,CD与点A,D.
(1)求∠BPC的度数;
(2)若![]() ,求AB+CD的值;
,求AB+CD的值;
(3)若![]() 为a,
为a,![]() 为b,
为b,![]() 为c,求证:a+b=c.
为c,求证:a+b=c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚,对市场最为关注的产量和产量的稳定性进行了抽样调查,过程如下:
收集数据从甲、乙两个大棚中分别随机收集了相同生产周期内25株秧苗生长出的小西红柿的个数:
甲:26,32,40,51,44,74,44,63,73,74,81,54,62,41,33,54,43,34,51,63,64,73,64,54,33
乙:27,35,46,55,48,36,47,68,82,48,57,66,75,27,36,57,57,66,58,61,71,38,47,46,71
整理数据按如下分组整理样本数据:
个数(x) 株数(株) 大棚 | 25≤x<35 | 35≤x<45 | 45≤x<55 | 55≤x<65 | 65≤x<75 | 75≤x<85 |
甲 | 5 |
| 5 |
| 4 | 1 |
乙 | 2 | 4 |
| 6 | 5 | 2 |
(说明:45个以下为产量不合格,45个及以上为产量合格,其中45≤x<65个为产量良好,65≤x<85个为产量优秀)
分析数据两组样本数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 众数 | 方差 |
甲 | 53 |
| 236.24 |
乙 | 53 | 57 | 215.04 |
得出结论
(1)补全上述表格;
(2)可以推断出 大棚的小西红柿秩苗品种更适应市场需求,理由为 (至少从两个不同的角度说明推断的合理性);
(3)估计乙大棚的300株小西红柿秧苗中产量优秀的有多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,B,与反比例函数图象的一个交点为
,B,与反比例函数图象的一个交点为![]() .
.
(1)求反比例函数的表达式;
(2)设直线![]() 与
与![]()
![]() 轴,
轴,![]() 轴分别交于点C,D,且
轴分别交于点C,D,且![]() ,直接写出
,直接写出![]() 的值 .
的值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(Ⅰ)如图1,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,抛物线
,抛物线![]() (
(![]() )经过
)经过![]() ,
,![]() ,
,![]() 三点.
三点.
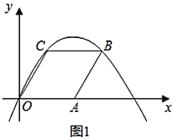
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________;
的坐标为__________;
(2)求抛物线的解析式.
(Ⅱ)如图2,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,直线
的中点,直线![]() 垂直
垂直![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上.
上.
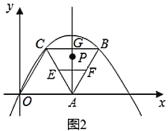
(3)当![]() 的值最小时,则点
的值最小时,则点![]() 的坐标为____________;
的坐标为____________;
(4)在(3)的条件下,连接![]() 、
、![]() 、
、![]() 得
得![]() ,问在抛物线上是否存在点
,问在抛物线上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
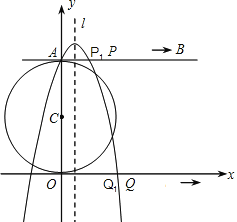
【题目】如图,在平面直角坐标系中,以点C(0,4)为圆心,半径为4的圆交y轴正半轴于点A,AB是⊙C的切线.动点P从点A开始沿AB方向以每秒1个单位长度的速度运动,点Q从O点开始沿x轴正方向以每秒4个单位长度的速度运动,且动点P、Q从点A和点O同时出发,设运动时间为t(秒).
(1)当t=1时,得到P1、Q1,求经过A、P1、Q1三点的抛物线解析式及对称轴l;
(2)当t为何值时,直线PQ与⊙C相切?并写出此时点P和点Q的坐标;
(3)在(2)的条件下,抛物线对称轴l上存在一点N,使NP+NQ最小,求出点N的坐标并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com