
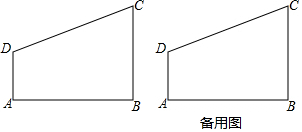
 已知,直角梯形ABCD中,∠B=90°,AD=1,BC=2,AB=3,点M位于线段AB上,且△DMC是直角三角形,求线段AM的长度.
已知,直角梯形ABCD中,∠B=90°,AD=1,BC=2,AB=3,点M位于线段AB上,且△DMC是直角三角形,求线段AM的长度. 分析 设AM=x.只要证明△AMD∽△BCM,可得$\frac{AM}{BC}$=$\frac{AD}{BM}$,构建方程即可解决问题.
解答 解:设AM=x.
∵∠A=∠B=∠DMC=90°,
∴∠AMD+∠BMC=90°,∠BMC+∠MCB=90°,
∴∠AMD=∠MCB,
∴△AMD∽△BCM,
∴$\frac{AM}{BC}$=$\frac{AD}{BM}$,
∴$\frac{x}{2}$=$\frac{1}{3-x}$,
解得x=1或2,经检验x=1或2是方程的解,
∴AM=1或2.
点评 本题考查直角梯形、相似三角形的判定和性质、一元二次方程等知识,解题的关键是学会利用相似三角形的性质,构建方程解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
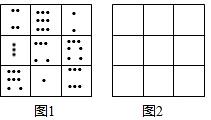 有人建议向火星发射如图1的图案.它叫做幻方,其中9个格中的点数分别是1,2,3,4,5,6,7,8,9.每一横行、每一竖列以及两条斜对角线上的点数的和都是15.如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).
有人建议向火星发射如图1的图案.它叫做幻方,其中9个格中的点数分别是1,2,3,4,5,6,7,8,9.每一横行、每一竖列以及两条斜对角线上的点数的和都是15.如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
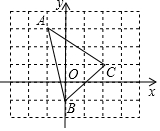 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,3),B(0,-1),C(2,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,3),B(0,-1),C(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com