
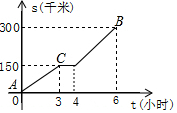
 杨师傅开车从A地出发去300千米远的B地游玩,其行驶路程s与时间t之间的关系如图所示,出发一段时间后,汽车发生故障,需停车检修,修好后又继续行驶.根据题意回答下列问题:
杨师傅开车从A地出发去300千米远的B地游玩,其行驶路程s与时间t之间的关系如图所示,出发一段时间后,汽车发生故障,需停车检修,修好后又继续行驶.根据题意回答下列问题:分析 (1)根据函数的图象可以知道横轴表示时间,纵轴表示路程,据此可以得到答案;
(2)观察图象可以得到汽车在3-4小时之间路程没有增加,说明此时在检修,由B地或C地的纵坐标即可得出答案;
(3)检修后两小时走了150千米据此可以求得速度.
解答 解:(1)路程与时间之间的关系.自变量是时间,因变量是路程;
(2)4-3=1(小时),300-150=150(千米),
汽车停车检修了1小时,修车的地方离B地还有150千米;
(3)(300-150)÷(6-4)=75(千米/小时),
车修好后的速度为75千米/小时.
点评 此题主要考查了看函数图象,解此类问题时,首先要看清横纵坐标所表示的意义.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
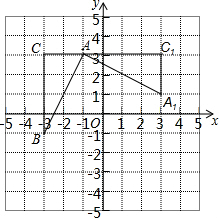 如图,在平面直角坐标系中,有一Rt△ABC,且点A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
如图,在平面直角坐标系中,有一Rt△ABC,且点A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
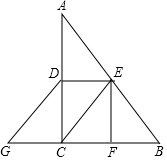 在△ABC中,∠ACB=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至点G,使CG=BF,连接CE,DE,DG.
在△ABC中,∠ACB=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至点G,使CG=BF,连接CE,DE,DG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com