Question

某高科技发展公司投资500万元，成功研制出一种市场需求量较大的高科技替代品，并投入资金1500万元进行批量生产．已知生产每件产品还需再投入40元，在销售过程中发现：当销售单价定为100元时，年销售量为20万件；销售单价每增加10元，年销售量将减少1万件，设销售单价为x（元），年销售量为y（万件），年获利为z（万元）．
（1）写出y与x及z与x的函数关系式；
（2）公司计划：在第一年按获利最大确定销售单价，进行销售；第二年年获利不低于1130万元，借助函数的说明，第二年的销售单价（元）应确定在什么范围内？

Answer 1

分析：（1）销售单价为x元，用x表示出年销售量和每件产品销售利润，利用每件产品销售利润×年销售量=年获利列出函数解答；
（2）利用配方法求得第一年按获利最大的销售单价，求得第二年的年获利函数，画出图象，利用图象解答即可．

解答：解：（1）依题意知，当销售单价为x元时，年销售量将减少

1

10

（x-100）万件，
因此y=20-

1

10

（x-100）=-

1

10

x+30，
z=（-

1

10

x+30）（x-40）-500-1500=-

1

10

x²+34x-3200；

（2）z=-

1

10

x²+34x-3200=-

1

10

（x-170）²-310；
因此当x=170时，z取得最大值-310，
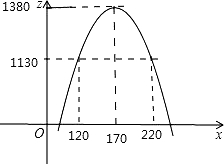
第二年的销售单价定为x元时，则年获利为
z=（-

1

10

x+30）（x-40）-310=-

1

10

x²+34x-1510；
当z=1130时，1130=-

1

10

x²+34x-1510，
解得x₁=120，x₂=220，
函数z=-

1

10

x²+34x-1510的图象大致如图：

由图象可知当120≤x≤220时，z≥1130．

点评：此题考查利用基本数量关系列二次函数，配方法的运用以及利用图象求一元二次不等式的解．