
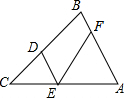
 如图,在△ABC中,∠B=70°,点D,E,F分别在BC,AC,AB上,且CD=CE,AF=AE,则∠DEF=55°.
如图,在△ABC中,∠B=70°,点D,E,F分别在BC,AC,AB上,且CD=CE,AF=AE,则∠DEF=55°. 分析 本题可先在△ABC中,根据三角形内角和定理求得∠A+∠C的度数,同理可求得∠CDE、∠CED、∠AEF、∠AFE四角的度数和,由于CD=DE、AF=AE,即可求出∠AEF和∠CED的度数和,由于这两个角和∠DEF互补,由此可求出∠DEF的度数.
解答 解:∠A+∠C=180°-70°=110°;
∴∠CDE+∠CED+∠AEF+∠AFE=360°-110°=250°;
∵CD=CE,AF=AE,
∴∠CDE=∠CED,∠AEF=∠AFE;
∴∠CED+∠AEF=125°;
∴∠DEF=55°.
故答案为:55°.
点评 本题综合考查了三角形的内角和定理以及等腰三角形的性质.利用了周角解题是正确解答本题的关键.


科目:初中数学 来源: 题型:解答题
 某单位准备将院内一块长30m,宽20m的长方形空土,建成一个矩形花园,要求在花园中修建两条纵向和一条横向的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?
某单位准备将院内一块长30m,宽20m的长方形空土,建成一个矩形花园,要求在花园中修建两条纵向和一条横向的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com