
如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12),动点P,Q分别从O、B两点同时出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,设动点P、Q运动时间为t(单位:s)
(1)当t为何值时,四边形PABQ是平行四边形,请写出推理过程;
(2)通过推理论证:在P、Q的运动过程中,线段DE的长度不变;
(1) ;(2)推理论证见解析.
;(2)推理论证见解析.
解析试题分析:(1)由PA∥BQ,知当AP=BQ时,四边形PABQ是平行四边形,所以根据AP=BQ列式求解即可;
(2)根据△BQD∽△OPD和△BDE∽△BOA列比例式即可证明.
试题解析:(1)∵PA∥BQ,∴当AP=BQ时,四边形PABQ是平行四边形.
根据题意,得13-2t=t,解得t= .
.
∴当t= 时,四边形PABQ是平行四边形.
时,四边形PABQ是平行四边形.
(2)∵OA∥BC,∴△BQD∽△OPD.∴ .∴
.∴ .
.
又∵DE∥OA,∴△BDE∽△BOA. ∴ .
.
又∵OA="13," ∴ (定值).
(定值).
∴在P、Q的运动过程中,线段DE的长度不变.
考点:1.双动点问题;2.平行四边形的性质;3.相似三角形的判定和性质.


科目:初中数学 来源: 题型:解答题
在Rt△ABC中,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,
且DM⊥DN,作MF⊥AB于点F,NE⊥AB于点E。
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC。
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,A(-1,1),B(-2,-1).(1)以原点O为位似中心,把线段AB放大到原来的2倍,请在图中画出放大后的线段CD;(2)在(1)的条件下,写出点A的对应点C的坐标为 ,点B的对应点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(1)如图1,在等边△ABC中,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等边△AMN,联结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是边BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.联结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,点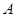 的坐标为
的坐标为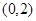 ,点
,点 在
在 轴上,
轴上, 是线段
是线段 的中点.将线段
的中点.将线段 绕着点
绕着点 顺时针方向旋转
顺时针方向旋转 ,得到线段
,得到线段 ,连结
,连结 、
、 .
.
(1)判断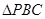 的形状,并简要说明理由;
的形状,并简要说明理由;
(2)当 时,试问:以
时,试问:以 、
、 、
、 、
、 为顶点的四边形能否为平行四边形?若能,求出相应的
为顶点的四边形能否为平行四边形?若能,求出相应的 的值?若不能,请说明理由;
的值?若不能,请说明理由;
(3)当 为何值时,
为何值时, 与
与 相似?
相似?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示.某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其余两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,每平方米投资6元;在△BHE、△FCG上都种花,每平方米投资10元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元.
(1)当FG长为多少米时,种草的面积与种花的面积相等?
(2)当矩形EFGH的边FG为多少米时,△ABC空地改造总投资最小,最小值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com