

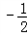 时,
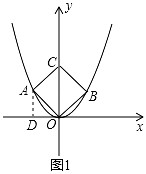
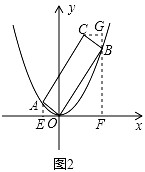
时,| 解:(1)如图,过点A作AD⊥x轴于点D, ∵矩形AOBC是正方形, ∴∠AOC=45°, ∴∠AOD=90°﹣45°=45°, ∴△AOD是等腰直角三角形, 设点A的坐标为(﹣a,a)(a≠0),则(﹣a)2=a, 解得a1=﹣1,a2=0(舍去), ∴点A的坐标﹣a=﹣1, 故答案为:﹣1; (2)①过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F, 当x=﹣  时,y=(﹣ 时,y=(﹣ )2= )2= , ,即OE=  ,AE= ,AE= , ,∵∠AOE+∠BOF=180°﹣90°=90°,∠AOE+∠EAO=90°, ∴∠EAO=∠BOF, 又∵∠AEO=∠BFO=90°, ∴△AEO∽△OFB, ∴ 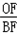 = =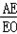 = =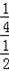 = = , ,设OF=t,则BF=2t, ∴t2=2t,解得:t1=0(舍去),t2=2, ∴点B(2,4); ②过点C作CG⊥BF于点G, ∵∠AOE+∠EAO=90°,∠FBO+∠CBG=90°,∠AEO=∠FBO,∴∠EAO=∠CBG, 在△AEO和△BGC中,  , ,∴△AEO≌△BGC(AAS), ∴CG=OE=  ,BG=AE= ,BG=AE= . .∴xc=2﹣  = = ,yc=4+ ,yc=4+ = = , ,∴点C(  , ,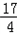 ), ),设过A(﹣  , , )、B(2,4)两点的抛物线解析式为y=﹣x2+bx+c, )、B(2,4)两点的抛物线解析式为y=﹣x2+bx+c,由题意得, 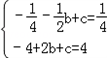 , ,解得 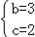 , ,∴经过A、B两点的抛物线解析式为y=﹣x2+3x+2, 当  x= x= 时,y=﹣( 时,y=﹣( )2+3× )2+3× +2= +2=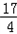 , ,所以点C也在此抛物线上, 故经过A、B、C三点的抛物线解析式为 y=﹣x2+3x+2=﹣(x﹣  )2+ )2+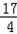 ; ;平移方案:先将抛物线y=﹣x2向右平移  个单位, 个单位,再向上平移 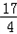 个单位得到抛物线y=﹣(x﹣ 个单位得到抛物线y=﹣(x﹣ )2+ )2+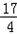 . . |
  |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
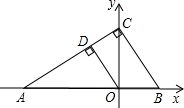 C作CB⊥AC,交x轴于B.
C作CB⊥AC,交x轴于B.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com