
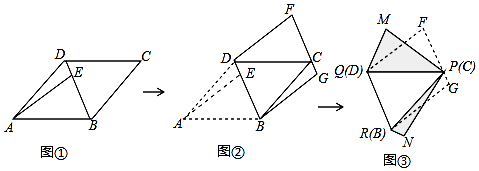
分析 根据平移和翻折的性质得到△MPN是等腰直角三角形,于是得到当PM最小时,对角线MN最小,即AE取最小值,当AE⊥BD时,AE取最小值,过D作DF⊥AB于F,根据平行四边形的面积得到DF=2,根据等腰直角三角形的性质得到AF=DF,由勾股定理得到BD=$\sqrt{D{F}^{2}+B{F}^{2}}$,根据三角形的面积得到AE的长,即可得到结论.
解答 解:∵△ABE≌△CDF≌△PMQ,
∴AE=DF=PM,∠EAB=∠FDC=∠MPQ,
∵△ADE≌△BCG≌△PNR,
∴AE=BG=PN,∠DAE=∠CBG=∠RPN,
∴PM=PN,
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB=45°,
∴∠MPN=90°,
∴△MPN是等腰直角三角形,
当PM最小时,对角线MN最小,即AE取最小值,
∴当AE⊥BD时,AE取最小值,
过D作DF⊥AB于F,
∵平行四边形ABCD的面积为28,AB=7,
∴DF=4,
∵∠DAB=45°,
∴AF=DF=4,
∴BF=3,
∴BD=$\sqrt{D{F}^{2}+B{F}^{2}}$=5,
∴AE=$\frac{DF•AB}{BD}$=$\frac{28}{5}$,
∴MN=$\sqrt{2}$AE=$\frac{28}{5}\sqrt{2}$,
故答案为:$\frac{28}{5}\sqrt{2}$.
点评 本题考查了平移的性质,翻折的性质,勾股定理,平行四边形的性质,正确的识别图形是解题的关键.


科目:初中数学 来源: 题型:填空题
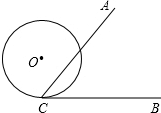 如图,∠ACB=60°,直径为4cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是2$\sqrt{3}$cm.
如图,∠ACB=60°,直径为4cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是2$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
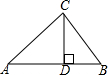 某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80米,BC=60米,若线段CD是一条小渠,且D点在边AB上,已知水果的造价为30元/米,问D点在距A点多远处时,水渠的造价最低?最低造价是多少?
某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80米,BC=60米,若线段CD是一条小渠,且D点在边AB上,已知水果的造价为30元/米,问D点在距A点多远处时,水渠的造价最低?最低造价是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
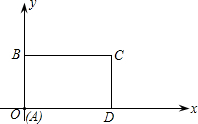 如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )| A. | a=2b | B. | a=3b | C. | a=4b | D. | a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com