
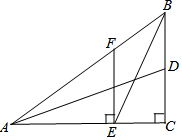
 如图△ABC中,∠ACB=90°,AB=10,BC=6,AC=8,BE是∠ABC的角平分线,AD是BC边的中线,EF⊥AC于点E,下列结论正确的有( )个
如图△ABC中,∠ACB=90°,AB=10,BC=6,AC=8,BE是∠ABC的角平分线,AD是BC边的中线,EF⊥AC于点E,下列结论正确的有( )个| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据高的定义即可判断;
②根据垂线段最短即可判断;
③求出∠BEC即可判断;
④如图作DE⊥AB于H.易知△ADH≌△ADC,可得AH=AC=8,BH=AB-AH=2,设DH=CD=x,在Rt△BDH中,可得方程22+x2=(6-x)2,解方程即可;
解答 解:①错误.EF不是△AEB中AE边上的高.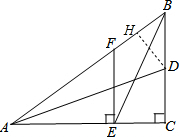
②正确.理由垂线段最短.
③错误.因为EF∥BC,所以∠AFE=∠ABC=54°,因为BE平分∠ABC,所以∠EBC=27°,推出∠BEC=63°.
④正确..如图作DE⊥AB于H.由△BDH∽△BAC,可得$\frac{BD}{AB}$=$\frac{DH}{AC}$,解得DH=2.4,故④正确.
点评 本题考查三角形的内角和定理、垂线段最短、点到直线的距离、三角形的角平分线、高、中线的定义、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:选择题
| A. | -4x<24与x<-6 | B. | 3x≤9与x-3≥0 | ||
| C. | 2x-7<6x与x<-$\frac{7}{4}$ | D. | -$\frac{1}{2}$x+3<0与$\frac{1}{3}$x-2>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c=2a | B. | a2+b2=c2 | C. | a:b=1:$\sqrt{3}$ | D. | b2=2a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
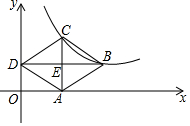 如图,菱形ABCD的顶点A在x轴上,D在y轴上,B、C在反比例函数的图象上,对角线AC、BD交于点E,且BD∥x轴,若AE=1,∠ADE=30°,则反比例函数的表达式为( )
如图,菱形ABCD的顶点A在x轴上,D在y轴上,B、C在反比例函数的图象上,对角线AC、BD交于点E,且BD∥x轴,若AE=1,∠ADE=30°,则反比例函数的表达式为( )| A. | $y=\frac{2}{x}$ | B. | $y=\frac{3}{x}$ | C. | $y=\frac{{\sqrt{3}}}{x}$ | D. | $y=\frac{{2\sqrt{3}}}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
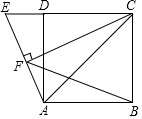 如图,在正方形ABCD中,点E在CD的延长线上,且CE=CA,连接AE,过点C作CF⊥AE于点F,连接BF.如果AB=4,则BF2的值为16+8$\sqrt{2}$.
如图,在正方形ABCD中,点E在CD的延长线上,且CE=CA,连接AE,过点C作CF⊥AE于点F,连接BF.如果AB=4,则BF2的值为16+8$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com