


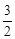 ,即DN=BM=
,即DN=BM=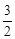 。
。
 。
。 。
。 。
。 ,CB=3,由勾股定理,得BQ=1。
,CB=3,由勾股定理,得BQ=1。 。∴PC=4-
。∴PC=4-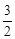 -
- =2。
=2。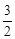 。过点N作NH⊥AB于H,则由勾股定理可得NM=
。过点N作NH⊥AB于H,则由勾股定理可得NM= ,从而根据平行四边形的性质和已知PQ=CQ,即可求得CQ=
,从而根据平行四边形的性质和已知PQ=CQ,即可求得CQ= 。因此,在△CBQ中,应用勾股定理求得BQ=1。从而求解。
。因此,在△CBQ中,应用勾股定理求得BQ=1。从而求解。

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A. | B.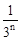 | C. | D.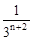 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
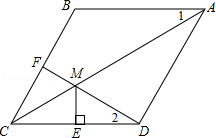
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com