
 已知:如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)相交于点A(2,3)和点B(6,m).
已知:如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)相交于点A(2,3)和点B(6,m).分析 (1)由A点坐标可求得k的值,把B点坐标代入反比例函数解析式可求得m的值;
(2)结合图象可知所求不等式即为直线在反比例函数图象上方时对应的自变量的取值范围,结合A、B坐标可求得答案;
(3)可设C点坐标为(x,0),由A、B两点坐标,则可表示出AC、BC的长,利用等腰直角三角形的性质和勾股定理可得到关于x的方程,可
解答 解:
(1)∵双曲线y=$\frac{k}{x}$(x>0)过点A(2,3),
∴k=2×3=6,
∴反比例函数解析式为y=$\frac{6}{x}$,
∵反比例函数图象过点B,
∴m=$\frac{6}{6}$=1;
(2)当ax+b>$\frac{k}{x}$时,即直线在反比例函数图象的上方时所对应的自变量的取值范围,
∵A(2,3),B(6,1),
∴当x>0且ax+b>$\frac{k}{x}$时,自变量的取值范围为2<x<6;
(3)设C点坐标为(x,0),
∴AC2=(x-2)2+32=x2-4x+13,BC2=(x-6)2+1=x2-12x+37,AB2=(6-2)2+(1-3)2=20,
∵△ABC为等腰直角三形,
∴∠ABC=90°、∠ACB=90°或∠CAB=90°三种情况,
①当∠ABC=90°时,则有AB2+BC2=AC2,即20+x2-12x+37=x2-4x+13,解得x=$\frac{11}{2}$,
但此时BC2=($\frac{11}{2}$)2-12×$\frac{11}{2}$+37=$\frac{5}{4}$≠20,即BC≠AB,故不符合题意;
②当∠ACB=90°时,则有AC2+BC2=AB2,即x2-12x+37+x2-4x+13=20,解得x=3或x=5,
当x=3时,x2-12x+37=10,x2-4x+13=10,即AC=BC,故符合题意;
当x=5时,x2-12x+37=2,x2-4x+13=18,即AC≠BC,故不符合题意;
∴C(3,0);
③当∠CAB=90°时,则有AC2+AB2=BC2,即20+x2-4x+13=x2-12x+37,解得x=$\frac{1}{2}$,
此时AC2=($\frac{1}{2}$)2-4×$\frac{1}{2}$+13=$\frac{45}{4}$≠20,即AC≠AB,故不符合题意;
综上可知存在满足条件的点C,其坐标为(3,0).
点评 本题为反比例函数的综合应用,涉及函数图象点的坐标特征、待定系数法、勾股定理、等腰三角形的性质、方程思想、数形结合思想及分类讨论思想等知识.在(1)中注意待定系数法的应用,在(2)中注意数形结合思想的应用,在(3)中用C点坐标分别表示出△ABC三边的长是解题的关键,注意分情况讨论.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
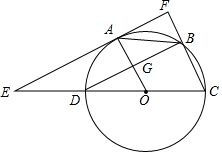 如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.
如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 83×10 | B. | 8.3×102 | C. | 8.3×103 | D. | 0.83×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 把一个正方体木块的表面涂上红色,将该正方体木块分割成x个大小相同的小正方体,如图所示,再将这些小正方体均匀地混合在一起,然后从中任意取出一个,若取到的小正方体两面有红色的概率为$\frac{4}{9}$,则x的取值为( )
把一个正方体木块的表面涂上红色,将该正方体木块分割成x个大小相同的小正方体,如图所示,再将这些小正方体均匀地混合在一起,然后从中任意取出一个,若取到的小正方体两面有红色的概率为$\frac{4}{9}$,则x的取值为( )| A. | 8 | B. | 27 | C. | 54 | D. | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com