
| A. | M<N | B. | M>N | ||
| C. | M=N | D. | M、N的大小关系不确定 |
分析 根据题意,对M和N作差,然后与零比较大小即可解答本题.
解答 解:由题意可得,xn+yn=9,
∴yn=(9-xn),
∴M-N=x12+x22+…+x102-(y12+y22+…+y102)
=x12+x22+…+x102-$(9-{x}_{1})^{2}-(9-{x}_{2})^{2}-…-(9-{x}_{10})^{2}$,
=-810+18(x1+x2+…+x10),
∵10名运动员参加乒乓球比赛,其中每两名恰好比赛一场,比赛中,没有平局,
x1+x2+…+x10=45,
∴-810+18(x1+x2+…+x10)=-810+18×45=-810+810=0,
∴M=N,
故选C.
点评 本题考查因式分解的应用,解题的关键是明确题意,找出所求问题需要的条件.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
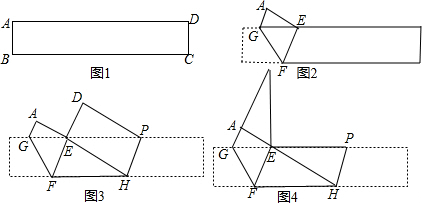
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小王同学的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站如乙下车,最后步行到学校(在整个过程中小丽步行的速度不变).图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
小王同学的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站如乙下车,最后步行到学校(在整个过程中小丽步行的速度不变).图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{8}$ | B. | $\root{3}{2}$ | C. | $\sqrt{8}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com