练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．Rt△ABC中，∠C=90°，tanA=$\frac{4}{3}$，AC=6cm，那么BC等于（　　）
    A．8cmB．$\frac{24}{5}$cmC．$\frac{18}{5}$cmD．$\frac{6}{5}$cm

    分析 根据锐角三角函数可以求得BC的长，从而可以解答本题．

    解答 解：∵Rt△ABC中，∠C=90°，tanA=$\frac{4}{3}$，AC=6cm，
    ∴tanA=$\frac{BC}{AC}=\frac{BC}{6}=\frac{4}{3}$，
    解得，BC=8，
    故选A．

    点评 本题考查解直角三角形，解题的关键是明确题意，找出所求问题需要的条件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．已知关于x的方程mx2-（3m-1）x+2m-2=0
    （1）求证：无论m取任何实数时，方程恒有实数根；
    （2）若关于x的二次函数y=mx2-（3m-1）x+2m-2的图象与x轴两个交点的横坐标均为整数，求m的整数值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：
    （1）$\sqrt{8}$-4$\sqrt{\frac{1}{8}}$+$\sqrt{32}$             
    （2）$\sqrt{2}$（$\sqrt{6}$-$\sqrt{2}$）+（$\sqrt{2}$-$\sqrt{3}$）（$\sqrt{2}$+$\sqrt{3}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，AB=AC，AD=AE，∠BAC=∠DAE，∠1=21°，∠2=30°，∠3=51°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．三个数：|-$\frac{7}{8}$|、+（-$\frac{6}{7}$）、-|-1|的大小关系是（　　）
    A．+（-$\frac{6}{7}$）＜|-$\frac{7}{8}$|＜-|-1|B．-|-1|＜|-$\frac{7}{8}$|＜+（-$\frac{6}{7}$）C．-|-1|＜+（-$\frac{6}{7}$）＜|-$\frac{7}{8}$|D．|-$\frac{7}{8}$|＜+（-$\frac{6}{7}$）＜-|-1|

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知[2x3（2x-3）-x2]÷2x2=x（2x-1），求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．已知△ABC为等边三角形，BD为中线，延长BC至E，使CE=CD=3，连接DE，则DE=3$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

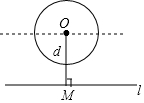    7．如图，给定一个半径长为2的圆，圆心O到水平直线l的距离为d，即OM=d．我们把圆上到直线l的距离等于1的点的个数记为m．如d=0时，l为经过圆心O的一条直线，此时圆上有四个到直线l的距离等于1的点，即m=4，由此可知：当m=2时，d的取值范围是1＜d＜3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．不改变分式的值，使下列分式的分子与分母都不含“-”号：
    （1）$\frac{a}{-2b}$
    （2）$\frac{-2x}{3y}$
    （3）$\frac{-2a}{-3b}$
    （4）-$\frac{{x}^{2}}{-2a}$．

    查看答案和解析>>

    同步练习册答案