
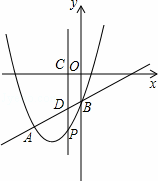
如图,抛物线y=x2+bx+c与直线y=x﹣1交于A、B两点.点A的横坐标为﹣3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
(1)求抛物线的解析式;
(2)当m为何值时,S四边形OBDC=2S△BPD;
(3)是否存在点P,使△PAD是直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
解:(1)∵y=x﹣1,∴x=0时,y=﹣1,∴B(0,﹣1).
当x=﹣3时,y=﹣4,∴A(﹣3,﹣4).
∵y=x2+bx+c与直线y=x﹣1交于A、B两点,∴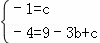 ,∴
,∴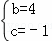 ,
,
∴抛物线的解析式为:y=x2+4x﹣1;
(2)∵P点横坐标是m(m<0),∴P(m,m2+4m﹣1),D(m,m﹣1)
如图1①,作BE⊥PC于E,
∴BE=﹣m.
CD=1﹣m,OB=1,OC=﹣m,CP=1﹣4m﹣m2,
∴PD=1﹣4m﹣m2﹣1+m=﹣3m﹣m2,
∴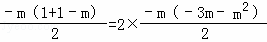 ,
,
解得:m1=0(舍去),m2=﹣2,m3=﹣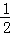 ;
;
如图1②,作BE⊥PC于E,
∴BE=﹣m.
PD=1﹣4m﹣m2+1﹣m=2﹣4m﹣m2,
∴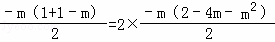 ,
,
解得:m=0(舍去)或m=﹣3,
∴m=﹣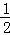 ,﹣2或﹣3时S四边形OBDC=2S△BPD;
,﹣2或﹣3时S四边形OBDC=2S△BPD;
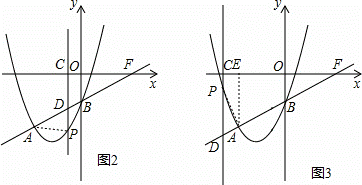
(3))如图2,当∠APD=90°时,设P(a,a2+4a﹣1),则D(a,a﹣1),
∴AP=m+4,CD=1﹣m,OC=﹣m,CP=1﹣4m﹣m2,
∴DP=1﹣4m﹣m2﹣1+m=﹣3m﹣m2.
在y=x﹣1中,当y=0时,x=1,∴(1,0),∴OF=1,
∴CF=1﹣m.AF=4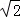 .∵PC⊥x轴,∴∠PCF=90°,
.∵PC⊥x轴,∴∠PCF=90°,
∴∠PCF=∠APD,∴CF∥AP,∴△APD∽△FCD,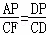 ,
,
∴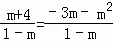 ,
,
解得:m=1舍去或m=﹣2,
∴P(﹣2,﹣5)
如图3,当∠PAD=90°时,作AE⊥x轴于E,
∴∠AEF=90°.CE=﹣3﹣m,EF=4,AF=4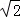 ,PD=1﹣m﹣(1﹣4m﹣m2)=3m+m2.
,PD=1﹣m﹣(1﹣4m﹣m2)=3m+m2.
∵PC⊥x轴,∴∠DCF=90°,∴∠DCF=∠AEF,∴AE∥CD.∴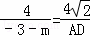 ,
,
∴AD=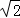 (﹣3﹣m).∵△PAD∽△FEA,∴
(﹣3﹣m).∵△PAD∽△FEA,∴ ,∴
,∴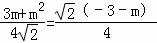 ,
,
∴m=﹣2或m=﹣3
∴P(﹣2,﹣5)或(﹣3,﹣4)与点A重合,舍去,
∴P(﹣2,﹣5).
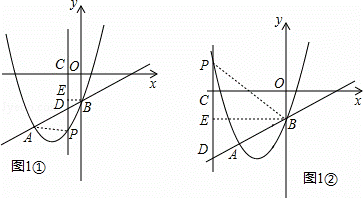


科目:初中数学 来源: 题型:
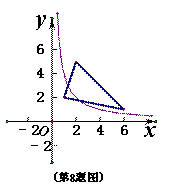
如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数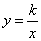 在第一象限内的图像与△ABC有交点,则
在第一象限内的图像与△ABC有交点,则 的取值范围是
的取值范围是
A.2≤ ≤
≤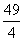 B.6≤
B.6≤ ≤10
≤10
C.2≤ ≤6 D.2≤
≤6 D.2≤ ≤
≤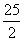
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的口袋里装有分别标有汉字“石”、“化”、“新”、“城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从袋中任取一个球,球上的汉字刚好是“新”的概率为多少?
(2)小明从袋中任取一球后,再任取一球,请用树状图或用列表的方法求出取出的两个球上的汉字能组成“石化”或“新城”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的一元二次方程x2﹣2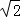 x+m=0,有两个不相等的实数根.
x+m=0,有两个不相等的实数根.
(1)求实数m的最大整数值;
(2)在(1)的条下,方程的实数根是x1,x2,求代数式x12+x22﹣x1x2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com