
分析 设去掉的数为x,根据一组自然数1,2,3…k,去掉其中一个数后剩下的数的平均数为16,得到1+2+3+…+k=16(k-1)+x=$\frac{k(k+1)}{2}$,从而得到1≤x=$\frac{k(k+1)}{2}$-16(k-1)=$\frac{1}{2}$(k2-31k+32)≤k,然后确定30≤k≤32,从而得解.
解答 解:设去掉的数为x,
∵一组自然数1,2,3…k,去掉其中一个数后剩下的数的平均数为16,
∴1+2+3+…+k=16(k-1)+x=$\frac{k(k+1)}{2}$,
∴x=1时,$\frac{k(k+1)}{2}$-1≥16(k-1),
x=k时,$\frac{k(k+1)}{2}$-k≤16(k-1),
即:30≤k≤32,
∴k=30,x=1,
k=31时,x=16,
k=32时,x=32
∴去掉的数是1,16,32.
故答案为:1,16,32.
点评 本题考查了算术平均数的知识,解题的关是根据题意得到1+2+3+…+k=16(k-1)+x=$\frac{k(k+1)}{2}$,难度不大.


科目:初中数学 来源: 题型:填空题
 如图,M、N是正方形ABCD中边AB、CD上的点,且AM≠DN,将正方形沿直线MN翻折180°.若正方形ABCD边长为1,则图中阴影部分的四个小三角形的周长和为4.
如图,M、N是正方形ABCD中边AB、CD上的点,且AM≠DN,将正方形沿直线MN翻折180°.若正方形ABCD边长为1,则图中阴影部分的四个小三角形的周长和为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
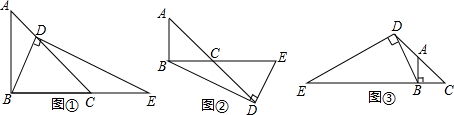
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的4×3网格中,每个小正方形的边长为1,正方形顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.
在如图所示的4×3网格中,每个小正方形的边长为1,正方形顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,不能判定DE∥CB的条件是( )
如图,在△ABC中,不能判定DE∥CB的条件是( )| A. | ∠ADE=∠ABC | B. | ∠DEB=∠CBE | C. | ∠BDE+∠ABC=180° | D. | ∠BDE=∠DEC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )| A. | ①④ | B. | ②③ | C. | ①③ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com