
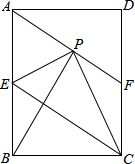
 如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,分析 (1)由折叠的性质得到BE=PE,EC与PB垂直,根据E为AB中点,得到AE=EB=PE,利用三角形内一边上的中线等于这条边的一半的三角形为直角三角形,得到∠APB为90°,进而得到AF与EC平行,再由AE与FC平行,利用两对边平行的四边形为平行四边形即可得证;
(2)根据三角形AEP为等边三角形,得到三条边相等,三内角相等,再由折叠的性质及邻补角定义得到一对角相等,根据同角的余角相等得到一对角相等,再由AP=EB,利用AAS即可得证;
(3)过P作PM⊥CD,在直角三角形EBC中,利用勾股定理求出EC的长,利用面积法求出BQ的长,根据BP=2BQ求出BP的长,在直角三角形ABP中,利用勾股定理求出AP的长,根据AF-AP求出PF的长,由PM与AD平行,得到三角形PMF与三角形ADF相似,由相似得比例求出PM的长,再由FC=AE=3,求出三角形CPF面积即可.
解答 (1)证明:由折叠得到BE=PE,EC⊥PB,
∵E为AB的中点,
∴AE=EB=PE,
∴AP⊥BP,
∴AF∥EC,
∵AE∥FC,
∴四边形AECF为平行四边形;
(2)∵△AEP为等边三角形,
∴∠BAP=∠AEP=60°,AP=AE=EP=EB,
∵∠PEC=∠BEC,
∴∠PEC=∠BEC=60°,
∵∠BAP+∠ABP=90°,∠ABP+∠BEQ=90°,
∴∠BAP=∠BEQ,
在△ABP和△EBC中,
$\left\{\begin{array}{l}{∠APB=∠EBC=90°}\\{∠BAP=∠BEQ}\\{AP=EB}\end{array}\right.$,
∴△ABP≌△EBC(AAS),
∵△EBC≌△EPC,
∴△ABP≌△EPC;
(3)过P作PM⊥DC,交DC于点M,
在Rt△EBC中,EB=3,BC=4,
根据勾股定理得:EC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵S△EBC=$\frac{1}{2}$EB•BC=$\frac{1}{2}$EC•BQ,
∴BQ=$\frac{3×4}{5}$=$\frac{12}{5}$,
由折叠得:BP=2BQ=$\frac{24}{5}$,
在Rt△ABP中,AB=6,BP=$\frac{24}{5}$,
根据勾股定理得:AP=$\sqrt{A{B}^{2}-B{P}^{2}}$=$\frac{18}{5}$,
∵四边形AECF为平行四边形,
∴AF=EC=5,FC=AE=3,
∴PF=5-$\frac{18}{5}$=$\frac{7}{5}$,
∵PM∥AD,
∴$\frac{PF}{AF}$=$\frac{PM}{AD}$,即$\frac{\frac{7}{5}}{5}$=$\frac{PM}{4}$,
解得:PM=$\frac{28}{25}$,
则S△PFC=$\frac{1}{2}$FC•PM=$\frac{1}{2}$×3×$\frac{28}{25}$=$\frac{42}{25}$.
点评 此题属于四边形综合题,涉及的知识有:全等三角形的判定与性质,折叠的性质,三角形内一边上的中线等于这条边的一半的三角形为直角三角形,等边三角形的性质,勾股定理,三角形的面积求法,相似三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 40人 | B. | 400人 | C. | 480人 | D. | 500人 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
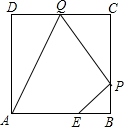 如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是$\frac{9}{2}$.
如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是$\frac{9}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com